【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=AC.

(1)求∠CDE的度数;
(2)若点M在DE上,且DC=DM,求证:ME=BD.
参考答案:
【答案】(1)60°(2)证明见解析
【解析】
(1)证明△ACD≌△BCD即可解题;(2)连接CM,先证明CM=CD,即可证明△BCD≌△ECM,即可解题.
(1)∵AC=BC,∠CAD=∠CBD,
∴∠DAB=∠DBA,
∴AD=BD,
在△ACD和△BCD中,
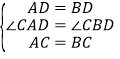 ,
,
∴△ACD≌△BCD(SAS),
∴∠ACD=∠BCD=45°,
∴∠CDE=∠CAD+∠ACD=60°;
(2)连接CM,
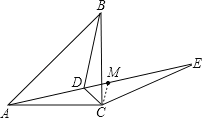
∵DC=DM,∠CDE=60°,
∴△DMC为等边三角形,
∴∠MCE=45°,
∴CM=CD,
在△BCD和△ECM中,
 ,
,
∴△BCD≌△ECM(SAS),
∴ME=BD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是高,CE是中线,点G是CE的中点,DG⊥CE,点G为垂足.

(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD,CE是△ABC的两条高,直线BD,CE相交于点H.

(1)若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中∠BAC=50°,直接写出∠DHE的度数是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,AD⊥BC于点D,以AD为一边向右作等边三角形ADE,DE与AC交于点F.
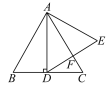
(1)试判断DF与EF的数量关系,并给出证明;
(2)若CF的长为2 cm,试求等边三角形ABC的边长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC,△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)在图①中,请你通过观察、测量、猜想,写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP,BQ,猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线l向左平移到图③的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,你认为(2)中所猜想的BQ与AP的数量关系与位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲同学手中藏有三张分别标有数字
 、
、  、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
、1的卡片,乙同学手中藏有三张分别标有数字1、3、2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为a,b.
(1)请你用树形图或列表法列出所有可能的结果;
(2)现制定一个游戏规则:若所选出的a,b能使得ax2+bx+1=0有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请用概率知识解释. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D、E分别是BC、AC上的点,BD=CE,求∠AFE的度数.
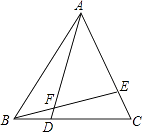
相关试题

