【题目】综合题。
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.
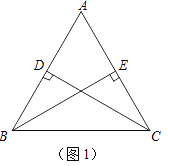
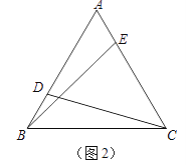
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
参考答案:
【答案】(1)证明见解析(2)CD=BE
【解析】试题分析:(1)利用AAS证明△ABE≌△ACD,利用全等三角形的性质即可证得结论;(2)分别作CF⊥AB,BG⊥AC,CD=BE,利用AAS证明△FBC≌△GCB,根据全等三角形的对应边相等可得CF=BG;再证得∠ADC=∠BEG,利用AAS证明△CFD≌△BGE,根据全等三角形的对应边相等即可得结论.
试题解析:
(1)证明:∵CD⊥AB于点D,BE⊥AC,
∴∠AEB=∠ADC=90°,
在△ABE与△ACD中, 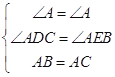 ,
,
∴△ABE≌△ACD(AAS).
∴CD=BE
(2)CD=BE, 证明如下:分别作CF⊥AB,BG⊥AC,
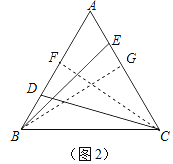
∴∠CBF=90°,∠BGC=90°,
∵AB=AC,
∴∠ABC=∠ACB,
在△FBC和△GCB中, 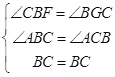 ,
,
∴△FBC≌△GCB.
∴CF=BG,
∵∠ADC+∠AEB=180°,
又∵∠BEG+∠AEB=180°,
∴∠ADC=∠BEG,
在△CFD和△BGE中, 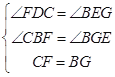 ,
,
∴△CFD≌△BGE,
∴CD=BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D。已知A(-1,0),C(0,3)
求抛物线的解析式;
在抛物线的对称轴上是否存在P点,使⊿PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标,如果不存在,请说明理由;
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,
①求直线BC 的解析式
②当点E运动到什么位置时,四边形CDBF的面积最大?求四边形CDBF的最大面积及此时点E的坐标

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=
 .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数

(1)若两点P(﹣3,m)和Q(1,m)在该函数图象上.求b、m的值;
(2)设该函数的顶点为点B,求出点B 的坐标并求三角形BPQ的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个凸 n 边形,其每个外角都等于30°,则n =______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据爱因斯坦的相对论,当地面上经过1秒钟时,宇宙飞船内只经过
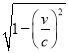 秒.公式内的v是指宇宙飞船的速度,c是指光速(约 30万千米/秒),假定有一对亲兄弟,哥哥23岁,弟弟 20岁,哥哥乘着以光速0. 98倍的速度飞行的宇宙飞船进行了5年宇宙旅行后回来了.这个5年是指地面上的5年,所以弟弟的年龄为25岁,可是哥哥的年龄在这段时间里只长了一岁,只有24岁,就这样,宇宙旅行后弟弟比哥哥反而大了1岁,请你用以上公式验证一下这个结论.
秒.公式内的v是指宇宙飞船的速度,c是指光速(约 30万千米/秒),假定有一对亲兄弟,哥哥23岁,弟弟 20岁,哥哥乘着以光速0. 98倍的速度飞行的宇宙飞船进行了5年宇宙旅行后回来了.这个5年是指地面上的5年,所以弟弟的年龄为25岁,可是哥哥的年龄在这段时间里只长了一岁,只有24岁,就这样,宇宙旅行后弟弟比哥哥反而大了1岁,请你用以上公式验证一下这个结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊿ABC的三个顶点都在格点上,
(1)画出⊿ABC关于x轴对称的⊿A1B1C1.
(2)画出⊿ABC绕原点O旋转180°后的⊿A2B2C2,并写出A2、B2、C2的坐标
(3)假设每个正方形网格的边长为1,求⊿A1B1C1.的面积。

相关试题

