【题目】如图,抛物线y=-x2+mx+n与x轴交于A,B两点,y与轴交于点C,抛物线的对称轴交x轴于点D。已知A(-1,0),C(0,3)
求抛物线的解析式;
在抛物线的对称轴上是否存在P点,使⊿PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标,如果不存在,请说明理由;
点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,
①求直线BC 的解析式
②当点E运动到什么位置时,四边形CDBF的面积最大?求四边形CDBF的最大面积及此时点E的坐标

参考答案:
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)P1(
x+2;(2)P1(![]() ,4),P2(
,4),P2(![]() ,
, ![]() ),P3(
),P3(![]() ,﹣
,﹣![]() );(3)①y=﹣
);(3)①y=﹣![]() x+2.②S四边形CDBF的面积最大=
x+2.②S四边形CDBF的面积最大=![]() ;E(2,1)
;E(2,1)
【解析】试题分析:(1)由待定系数法建立二元一次方程组求出m、n的值即可;
(2)如图1中,分两种情形讨论①当PD=DC时,当CP=CD时,分别写出点P坐标即可.
(3)先求出BC的解析式,设出点E的横坐标为a,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF求出S与a的关系式,由二次函数的性质就可以求出结论.
试题解析:(1)∵抛物线y=-![]() x2+mx+n经过A(-1,0),C(0,2).
x2+mx+n经过A(-1,0),C(0,2).
解得: 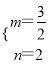 ,
,
∴抛物线的解析式为:y=-![]() x2+
x2+![]() x+2;
x+2;
(2)如图1,

∵y=-![]() x2+
x2+![]() x+2,
x+2,
∴y=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∴抛物线的对称轴是直线x=![]() .
.
∴OD=![]() .
.
∵C(0,3),
∴OC=23
在Rt△OCD中,由勾股定理,得CD=![]() .
.
∵△CDP是以CD为腰的等腰三角形,
∴CP1=DP2=DP3.
作CH⊥x轴于H,
∴HP1=HD=2,
∴DP1=4.
∴P1(![]() ,4),P2(
,4),P2(![]() ,
, ![]() ),P3(
),P3(![]() ,-
,-![]() );
);
(3)当y=0时,0=-![]() x2+
x2+![]() x+2
x+2
∴x1=-1,x2=4,
∴B(4,0).
设直线BC的解析式为y=kx+b,由图象,得![]() ,
,
解得: 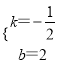 ,
,
∴直线BC的解析式为:y=-![]() x+2.
x+2.
如图2,

过点C作CM⊥EF于M,设E(a,-![]() a+2),F(a,-
a+2),F(a,-![]() a2+
a2+![]() a+2),
a+2),
∴EF=-![]() a2+
a2+![]() a+2-(-
a+2-(-![]() a+2)=-
a+2)=-![]() a2+2a(0≤x≤4).
a2+2a(0≤x≤4).
∵S四边形CDBF=S△BCD+S△CEF+S△BEF=![]() BDOC+
BDOC+![]() EFCM+
EFCM+![]() EFBN,
EFBN,
=![]() ×
×![]() ×2+
×2+![]() a(-
a(-![]() a2+2a)+
a2+2a)+![]() (4-a)(-
(4-a)(-![]() a2+2a),
a2+2a),
=-a2+4a+![]() (0≤x≤4).
(0≤x≤4).
=-(a-2)2+![]()
∴a=2时,S四边形CDBF的面积最大=![]() ,
,
∴E(2,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某班学生每天使用零花钱的情况,小红随机调查了15名同学,结果如下表:
每天使用零花钱
(单位:元)1
2
3
5
6
人 数
2
5
4
3
1
则这15名同学每天使用零花钱的众数和中位数分别是( )
A.3,3
B.2,3
C.2,2
D.3,5 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,假命题是( )
A. 菱形的面积等于两条对角线乘积的一半
B. 矩形的对角线相等
C. 对角线互相垂直的平行四边形是矩形
D. 对角线相等的菱形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下长度的三条线段,不能组成三角形的是( )
A. 3、8、2 B. 2、5、4 C. 6、3、5 D. 9、15、7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=
 .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数

(1)若两点P(﹣3,m)和Q(1,m)在该函数图象上.求b、m的值;
(2)设该函数的顶点为点B,求出点B 的坐标并求三角形BPQ的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)如图1,在△ABC中,AB=AC,CD⊥AB于D,BE⊥AC于E,试证明:CD=BE.
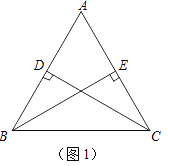
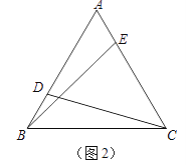
(2)如图2,在△ABC中,仍然有条件“AB=AC,点D,E分别在AB和AC上”.若∠ADC+∠AEB=180°,则CD与BE是否仍相等?若相等,请证明;若不相等,请举反例说明.
相关试题

