【题目】综合与探究
如图,在平面直角坐标系中,![]() ,点
,点![]() .
.
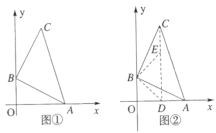
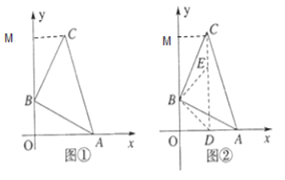
(1)在图①中,点![]() 坐标为__________;
坐标为__________;
(2)如图②,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,作等腰直角三角形
,作等腰直角三角形![]() ,
,![]() ,连接
,连接![]() .证明:
.证明:![]() ;
;
(3)在图②的条件下,若![]() 三点共线,求
三点共线,求![]() 的长;
的长;
(4)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 面积为2.请直接写出所有满足条件的点
面积为2.请直接写出所有满足条件的点![]() 的坐标.
的坐标.
参考答案:
【答案】(1)(1,3);
(2)答案见解析;
(3)OD=1
(4)F的坐标是![]() 或
或![]()
【解析】
(1)过C点作![]() 轴,垂足为F,在证明了
轴,垂足为F,在证明了![]() 后可得到线段BM、CM的长,再求出线段OM的长,便可得点C的坐标;
后可得到线段BM、CM的长,再求出线段OM的长,便可得点C的坐标;
(2)根据![]() 和等式的基本性质证明
和等式的基本性质证明![]() ,再利用“SAS”定理证明
,再利用“SAS”定理证明![]() 后便可得到
后便可得到![]() ;
;
(3) ![]() 三点共线时,
三点共线时,![]() 可推导出
可推导出![]() 轴,从而有
轴,从而有![]() ;
;
(4)根据点F在y轴上,所以![]() 中BF上的高总是OA=2,在此处只需要利用其面积为2和三角形的面积计算:
中BF上的高总是OA=2,在此处只需要利用其面积为2和三角形的面积计算:![]() ,分点F在点B的上方和下方两种情况讨论可得.
,分点F在点B的上方和下方两种情况讨论可得.
(1)过点C作![]() 轴,垂足为M,则
轴,垂足为M,则![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
∴![]() ,
, ![]()
∵点![]()
∴![]() ,
, ![]()
∴![]()
而点C在第一象限,所以点![]()
(2)∵![]() 等腰直角三角形
等腰直角三角形
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
(3)由(2) ![]() 可得
可得![]()
∵![]() 三点共线且三角形
三点共线且三角形![]() 是等腰直角三角形
是等腰直角三角形
∴![]()
∴![]()
又![]()
∴四边形ODCM是矩形
∴![]()
(4)∵点F在y轴上
∴![]() 的边BF的高为OA=2
的边BF的高为OA=2
∵![]()
即 ![]()
∴![]()
当点F在点B的上方时,其坐标为(3,0);
当点F在点B的下方时,其坐标为(-1,0).
故点F的坐标为(3,0)或(-1,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在直角梯形ABCD中,AB⊥BC,AD∥BC,点P为DC上一点,且AP=AB,过点C作CE⊥BP交直线BP于E.
(1) 若
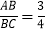 ,求证:
,求证: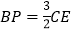 ;
;(2) 若AB=BC.
① 如图2,当点P与E重合时,求
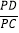 的值;
的值;② 如图3,设∠DAP的平分线AF交直线BP于F,当CE=1,
 时,直接写出线段AF的长.
时,直接写出线段AF的长.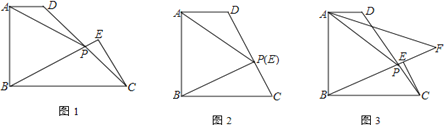
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合实践
如图①,
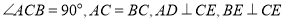 ,垂足分别为点
,垂足分别为点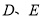 ,
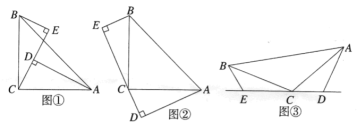
,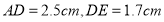 .
.
(1)求
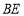 的长;
的长;(2)将
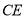 所在直线旋转到
所在直线旋转到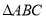 的外部,如图②,猜想
的外部,如图②,猜想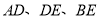 之间的数量关系,直接写出结论,不需证明;
之间的数量关系,直接写出结论,不需证明;(3)如图③,将图①中的条件改为:在
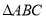 中,
中,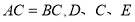 三点在同一直线上,并且
三点在同一直线上,并且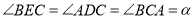 ,其中
,其中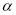 为任意钝角.猜想
为任意钝角.猜想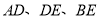 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
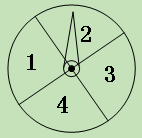
查看答案和解析>>【题目】(11·孝感)学生甲与学生乙玩一种转盘游戏.如图是两个完全相同的转盘,每个转盘被分成面积相等的四个区域,分别用数字“1”、“2”、“3”、“4”表示.固定指针,同时转动两个转盘,任其自由停止,若两指针所指数字的积为奇数,则甲获胜;若两指针所指数字的积为偶数,则乙获胜;若指针指向扇形的分界线,则都重转一次.在该游戏中乙获胜的概率是 ( )
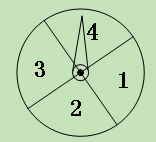
A.
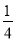 B.
B.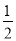 C.
C.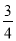 D.
D.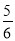
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB = 6cm,AD=10 cm,点P在AD 边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止 (同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
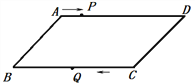
A. 1 次 B. 2次 C. 3次 D. 4次
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
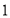 的菱形
的菱形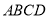 中,
中,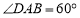 .连结对角线
.连结对角线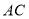 ,以
,以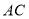 为边作第二个菱形
为边作第二个菱形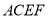 ,使
,使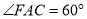 .连结
.连结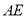 ,再以
,再以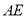 为边作第三个菱形
为边作第三个菱形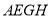 ,使
,使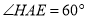 ,一按此规律所作的第
,一按此规律所作的第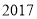 个菱形的边长是__________.
个菱形的边长是__________.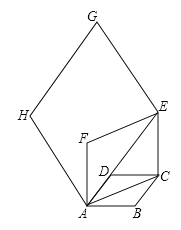
-
科目: 来源: 题型:
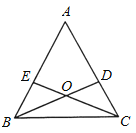
查看答案和解析>>【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
相关试题

