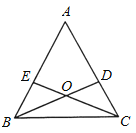
【题目】如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的角平分线,且BD和CE相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
参考答案:
【答案】(1)详见解析;(2)直线AO垂直平分BC
【解析】
(1)根据对边对等角得到∠ABC=∠ACB,再结合角平分线的定义得到∠OBC=∠OCB,从而证明OB=OC;
(2)首先根据全等三角形的判定和性质得到OA平分∠BAC,再根据等腰三角形的三线合一的性质得到直线AO垂直平分BC.
(1)∵ 在△ABC中,AB=AC,
∴ ∠ABC=∠BCA,
∵ BD、CE分别平分∠ABC、∠BCA,
∴ ∠ABD=∠CBD ,∠ACE=∠BCE,
∴ ∠OBC=∠BCO,
∴ OB=OC,
∴ △OBC为等腰三角形;
(2)在△AOB与△AOC中,
∵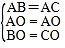 ,
,
∴△AOB≌△AOC(SSS),
∴∠BAO=∠CAO,∴直线AO垂直平分BC.(等腰三角形顶角的平分线、底边上的高、底边上的中线互相重合)
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
如图,在平面直角坐标系中,
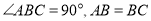 ,点
,点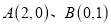 .
.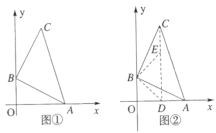
(1)在图①中,点
 坐标为__________;
坐标为__________;(2)如图②,点
 在线段
在线段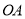 上,连接
上,连接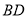 ,作等腰直角三角形
,作等腰直角三角形 ,
,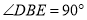 ,连接
,连接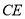 .证明:
.证明: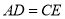 ;
;(3)在图②的条件下,若
 三点共线,求
三点共线,求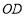 的长;
的长;(4)在
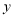 轴上找一点
轴上找一点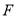 ,使
,使 面积为2.请直接写出所有满足条件的点
面积为2.请直接写出所有满足条件的点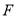 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB = 6cm,AD=10 cm,点P在AD 边上以每秒1 cm的速度从点A向点D运动,点Q在BC边上,以每秒4 cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止 (同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
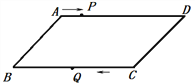
A. 1 次 B. 2次 C. 3次 D. 4次
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为
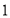 的菱形
的菱形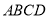 中,
中,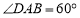 .连结对角线
.连结对角线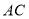 ,以
,以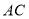 为边作第二个菱形
为边作第二个菱形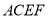 ,使
,使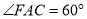 .连结
.连结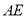 ,再以
,再以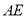 为边作第三个菱形
为边作第三个菱形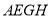 ,使
,使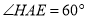 ,一按此规律所作的第
,一按此规律所作的第 个菱形的边长是__________.
个菱形的边长是__________.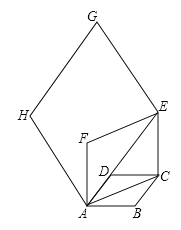
-
科目: 来源: 题型:
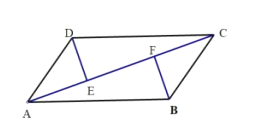
查看答案和解析>>【题目】如图,已知
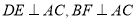 ,垂足分别是
,垂足分别是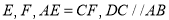 .
.
(1)证明:
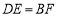 .
.(2)连接
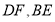 ,猜想
,猜想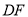 与
与 的关系?并证明你的猜想的正确性.
的关系?并证明你的猜想的正确性. -
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接“均衡教育大检查”,县委县府对通往某偏远学校的一段全长为1200 米的道路进行了改造,铺设草油路面.铺设400 米后,为了尽快完成道路改造,后来每天的工作效率比原计划提高25%,结果共用13天完成道路改造任务.
(1)求原计划每天铺设路面多少米;
(2)若承包商原来每天支付工人工资为1500元,提高工作效率后每天支付给工人的工资增长了20%,完成整个工程后承包商共支付工人工资多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m3)是体积V(单位:m3)的反比例函数,它的图象如图所示,当V=10m3时,气体的密度是( )
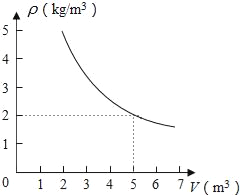
A. 1kg/m3 B. 2kg/m3 C. 100kg/m3 D. 5kg/m3
相关试题

