【题目】某中学开展“绿化家乡、植树造林”活动,为了解全校植树情况,对该校甲、乙、丙、丁四个班级植树情况进行了调查,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
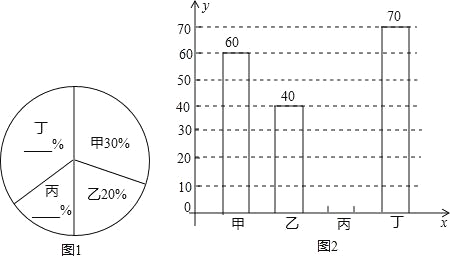
(1)这四个班共植树 棵;
(2)请你在答题卡上不全两幅统计图;
(3)求图1中“甲”班级所对应的扇形圆心角的度数;
(4)若四个班级植树的平均成活率是95%,全校共植树2000棵,请你估计全校种植的树中成活的树有多少棵?
参考答案:
【答案】(1)200;(2)补图见解析.(3)108°;(4)1900.
【解析】
试题分析:(1)根据乙班植树40棵,所占比为20%,即可求出这四个班种树总棵数;
(2)根据丁班植树70棵,总棵数是200,即可求出丁所占的百分比,再用整体1减去其它所占的百分比,即可得出丙所占的百分比,再乘以总棵数,即可得出丙植树的棵数,从而补全统计图;
(3)根据甲班级所占的百分比,再乘以360°,即可得出答案;
(4)用总棵数×平均成活率即可得到成活的树的棵数.
试题解析:(1)四个班共植树的棵数是:
40÷20%=200(棵);
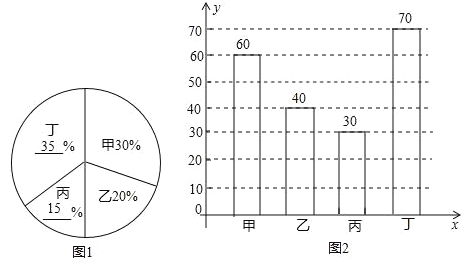
(2)丁所占的百分比是:![]() ×100%=35%,
×100%=35%,
丙所占的百分比是:1-30%-20%-35%=15%,
则丙植树的棵数是:200×15%=30(棵);
如图:
(3)甲班级所对应的扇形圆心角的度数是:30%×360°=108°;
(4)根据题意得:2000×95%=1900(棵).
答:全校种植的树中成活的树有1900棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
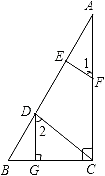
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC( )
∴∠2= ( )
∵∠1=∠2(已知)
∴∠1=∠ (等量代换)
∴EF∥CD( )
∴∠AEF=∠ ( )
∵EF⊥AB(已知)
∴∠AEF=90°( )
∴∠ADC=90°( )
∴CD⊥AB( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了参加中考体育测试,甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传球三次.
(1)请利用树状图列举出三次传球的所有可能情况;
(2)求三次传球后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,DE∥AB,EF∥AB,∠BED=∠CEF,
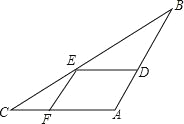
(1)试说明△ABC是等腰三角形,
(2)探索AB+AC与四边形ADEF的周长关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)a3(-b3)2+(-2ab2)3;
(2)(a-b)10÷(b-a)3÷(b-a)3;
(3)-22+(-
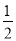 )-2-(π-5)0-|-4|;
)-2-(π-5)0-|-4|;(4)(x+y-3)(x-y+3);
(5)3x2y(2x-3y)-(2xy+3y2)(3x2-3y);
(6)(x-2y)(x+2y)-(x-2y)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】生物课题研究小组对附着在物体表面的三个微生物(课题组成员把他们分别标号为1,2,3)的生长情况进行观察记录,这三个微生物第一天各自一分为二,产生新的微生物(依次被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录),那么标号为1535的微生物会出现在( )
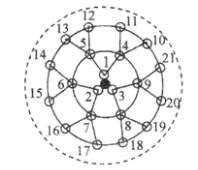
A.第7天 B.第8天 C.第9天 D.第10天
-
科目: 来源: 题型:
查看答案和解析>>【题目】向东行进﹣50m表示的意义是( )
A.向东行进50m
B.向南行进50m
C.向北行进50m
D.向西行进50m
相关试题

