【题目】已知二次函数y=mx2+nx+p图象的顶点横坐标是2,与x轴交于A(x1,0)、B(x2,0),x1<0<x2,与y轴交于点C,O为坐标原点,tan∠CAO﹣tan∠CBO=1.
(1)求证:n+4m=0;
(2)求m、n的值;
(3)当p>0且二次函数图象与直线y=x+3仅有一个交点时,求二次函数的最大值.
参考答案:
【答案】(1)证明见解析(2)m=![]() ,n=-1或m=-
,n=-1或m=-![]() ,n=1(3)4
,n=1(3)4
【解析】
试题分析:(1)由题意可知抛物线的对称轴为x=2,利用对称轴公式x=![]() ,易证n+4m=0;
,易证n+4m=0;
(2)本问利用三角函数定义和抛物线与x轴交点坐标性质求解.特别需要注意的是抛物线的开口方向未定,所以所求m、n的值将有两组,不能遗漏;
(3)本问利用一元二次方程的判别式等于0求解.当p>0时,m、n的值随之确定;将抛物线的解析式与直线的解析式联立,得到一个一元二次方程;由交点唯一可知,此一元二次方程的判别式等于0,据此求出p的值,从而确定了抛物线的解析式;最后由抛物线的解析式确定其最大值.
试题解析:
(1)∵二次函数y=mx2+nx+p图象的顶点横坐标是2,
∴抛物线的对称轴为x=2,
即![]() =2,
=2,
化简得:n+4m=0.
(2)∵二次函数y=mx2+nx+p与x轴交于A(x1,0)、B(x2,0),x1<0<x2,
∴OA=﹣x1,OB=x2;
x1+x2=![]() ,x1x2=
,x1x2=![]() ;
;
令x=0,得y=p,
∴C(0,p),
∴OC=|p|.
由三角函数定义得:tan∠CAO=![]() ,tan∠CBO=
,tan∠CBO=![]() .
.
∵tan∠CAO﹣tan∠CBO=1
,即![]() ,
,
化简得:![]() =
=![]() ,
,
将x1+x2=![]() ,x1x2=
,x1x2=![]() 代入得:
代入得: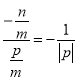 ,
,
化简得:n=![]() =±1.
=±1.
由(1)知n+4m=0,
∴当n=1时,m=-![]() ;当n=﹣1时,m=
;当n=﹣1时,m=![]() .
.
∴m、n的值为:m=![]() ,n=﹣1(此时抛物线开口向上)或m=-
,n=﹣1(此时抛物线开口向上)或m=-![]() ,n=1(此时抛物线开口向下).
,n=1(此时抛物线开口向下).
(3)解:由(2)知,当p>0时,n=1,m=-![]() ,
,
∴抛物线解析式为:y=![]() x2+x+p.
x2+x+p.
联立抛物线y=![]() x2+x+p与直线y=x+3解析式得到:
x2+x+p与直线y=x+3解析式得到: ![]() x2+x+p=x+3,
x2+x+p=x+3,
化简得:x2﹣4(p﹣3)=0 ①.
∵二次函数图象与直线y=x+3仅有一个交点,
∴一元二次方程①的判别式等于0,
即△=02+16(p﹣3)=0,解得p=3.
∴抛物线解析式为:y=![]() x2+x+p=y=
x2+x+p=y=![]() x2+x+3=
x2+x+3=![]() (x﹣2)2+4,
(x﹣2)2+4,
当x=2时,二次函数有最大值,最大值为4.
∴当p>0且二次函数图象与直线y=x+3仅有一个交点时,二次函数的最大值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若三角形三边长为整数,周长为11,且有一边长为4,则此三角形中最长的边是( )
A.7
B.6
C.5
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年我省粮食总产量695.2亿斤,居历史第二高位,695.2亿用科学记数法表示为:
A. 695.2×108 B. 6.952×109 C. 6.952×1010 D. 6.952×1011
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
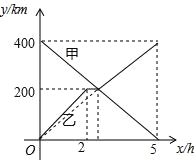
(1)乙车休息了 h.
(2)求乙车与甲车相遇后y乙关于x的函数表达式,并写出自变量x的取值范围.
(3)当两车相距40km时,求x的值.
-
科目: 来源: 题型:
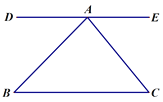
查看答案和解析>>【题目】如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
(1)求∠DAB的度数,并写出理由.
(2)求∠EAC的度数.
(3)计算∠BAC的度数.
(4)根据以上条件及结论,你还能得出其他结论吗?试写出一个.
-
科目: 来源: 题型:
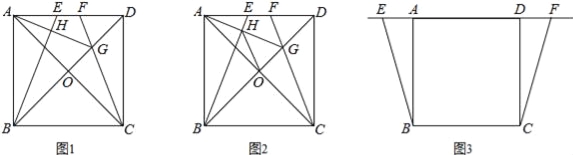
查看答案和解析>>【题目】四边形ABCD是正方形,AC与BD,相交于点O,点E、F是直线AD上两动点,且AE=DF,CF所在直线与对角线BD所在直线交于点G,连接AG,直线AG交BE于点H.
(1)如图1,当点E、F在线段AD上时,①求证:∠DAG=∠DCG;②猜想AG与BE的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接HO,试说明HO平分∠BHG;
(3)当点E、F运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出∠BHO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:2x2+4x+2=____________.
相关试题

