【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为____________,其解为x1=-4,x2=-5;
(2)根据这类方程特征,写出第n个方程为________________,其解为x1=-n,x2=-n-1;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
参考答案:
【答案】(1) x1=-4,x2=-5;(2)x1=-n,x2=-n-1;(3) x1=-n-3,x2=-n-4
【解析】试题分析:观察方程特点,可以得到数据的关系.
试题解析:
(1)x+![]() =-9 x1=-4,x2=-5;
=-9 x1=-4,x2=-5;
(2)x+![]() =-(2n+1)
=-(2n+1)
x1=-n,x2=-n-1;
(3)解:x+![]() =-2(n+2),
=-2(n+2),
x+3+![]() =-2(n+2)+3,
=-2(n+2)+3,
(x+3)+![]() =-(2n+1),
=-(2n+1),
∴x+3=-n或x+3=-n-1,
即x1=-n-3,x2=-n-4.
检验:当x=-n-3时,x+3=-n≠0,
当x=-n-4时,x+3=-n-1≠0,
∴原分式方程的解是x1=-n-3,x2=-n-4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)已知:如图1,四边形
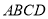 是“等对角四边形”,
是“等对角四边形”, 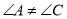 ,
, 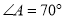 ,
, 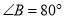 .求
.求 ,
, 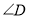 的度数.
的度数.(2)在探究“等对角四边形”性质时:
① 小红画了一个“等对角四边形”
 (如图2),其中
(如图2),其中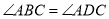 ,
,  ,此时她发现
,此时她发现 成立.请你证明此结论.
成立.请你证明此结论.② 由此小红猜想:“对于任意‘等对角四边形’,当一组邻边相等时,另一组邻边也相等”.你认为她的猜想正确吗?若正确,请证明;若不正确,请举出反例.
(3)已知:在“等对角四边形”
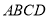 中,
中, 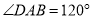 ,
,  ,AB=AD=4,.求∠D和对角线
,AB=AD=4,.求∠D和对角线 的长.
的长.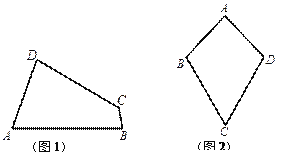
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在反比例函数y=
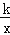 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )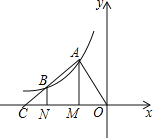
A.2 B.4 C.﹣2 D.﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得:
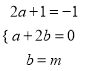 ,解得:
,解得: 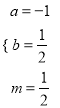 ,∴
,∴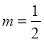 .
.解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取
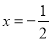 ,
, 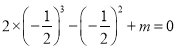 ,故
,故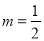 .
.(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件能保证△ABC≌△ADC的是:①AB=AD,BC=DC;②∠1=∠3,∠4=∠2;③∠1=∠2,∠4=∠3;④∠1=∠2,AB=AD;⑤∠1=∠2,BC=DC.( )
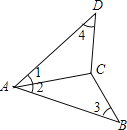
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
-
科目: 来源: 题型:
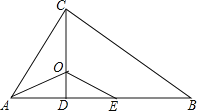
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,CD⊥AB于点D,AO平分∠BAC,交CD于点O,E为AB上一点,且AE=AC。
(1)求证:△AOC≌△A0E;
(2)求证:OE∥BC。
-
科目: 来源: 题型:
查看答案和解析>>【题目】图(1)是我们常见的“箭头图”,其中隐藏着哪些数学知识呢?下面请你解决以下问题:

(1)观察如图(1)“箭头图”,试探究∠BDC与∠A、∠B、∠C之间大小的关系,并说明理由;
(2)请你直接利用以上结论,回答下列两个问题:
①如图(2),把一块三角板XYZ放置在△ABC上,使其两条直角边XY、XZ恰好经过点B、C.若∠A=50°,则∠ABX+∠ACX= ;
②如图(3),∠ABD,∠ACD的五等分线分别相交于点G1、G2、G3、G4,若∠BDC=135°,∠BG1C=67°,求∠A的度数.
相关试题

