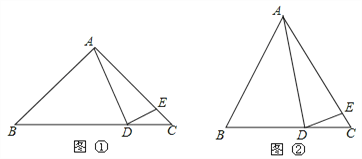
【题目】(14分)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
参考答案:
【答案】(1)30° (2) ∠CDE=![]() ∠BAD (3) ∠CDE=
∠BAD (3) ∠CDE=![]() ∠BAD
∠BAD
【解析】试题分析:(1)根据等腰三角形的性质得到∠CAD=∠BAD=60°,由于AD=AE,于是得到∠ADE=60°,根据三角形的内角和即可得到∠CDE=75°﹣45°=30°;
(2)设∠BAD=x,于是得到∠CAD=90°﹣x,根据等腰三角形的性质得到∠AED=45°+![]() ,于是得到结论;
,于是得到结论;
(3)设∠BAD=x,∠C=y,根据等腰三角形的性质得到∠BAC=180°﹣2y,由∠BAD=x,于是得到∠DAE=y+![]() x,即可得到结论.
x,即可得到结论.
解:(1)∵AB=AC,∠BAC=90°,
∴∠B=∠C=45°,
∵∠BAD=60°,
∴∠DAE=30°,
∵AD=AE,
∴∠AED=75°,
∴∠CDE=∠AED=∠C=30°;
(2)设∠BAD=x,
∴∠CAD=90°﹣x,
∵AE=AD,
∴∠AED=45°+![]() ,
,
∴∠CDE=![]() x;
x;
(3)设∠BAD=x,∠C=y,
∵AB=AC,∠C=y,
∴∠BAC=180°﹣2y,
∵∠BAD=x,
∴∠DAE=y+![]() x,
x,
∴![]() x.
x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+bx+c图象向右平移2个单位再向下平移3个单位,所得图象的解析式为y=x2﹣2x﹣3,则b、c的值为( )
A.b=2,c=2 B.b=2,c=0
C.b=﹣2,c=﹣1 D.b=﹣3,c=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(x+1)(3x﹣2)=0的一般形式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方法中,不能判定三角形全等的是( )
A. SSA B. SSS C. ASA D. SAS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )
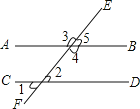
A.如果∠5=50°,那么AB∥CD B.如果∠4=130°,那么AB∥CD
C.如果∠3=130°,那么AB∥CD D.如果∠2=50°,那么AB∥CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,平方数的开平方运算可以直接求得,如
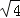 等,有些数则不能直接求得,如
等,有些数则不能直接求得,如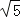 ,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:
,但可以通过计算器求得.还有一种方法可以通过一组数的内在联系,运用规律求得.请你观察下表:a … 0.04 4 400 40000 …
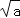 … x 2 y z …
… x 2 y z …(1)表格中的三个值分别为:x= ;y= ;z= ;
(2)用公式表示这一规律:当a=4×100n(n为整数)时,
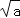 = ;
= ;(3)利用这一规律,解决下面的问题:
已知
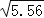 ≈2.358,则①
≈2.358,则①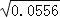 ≈ ;②
≈ ;②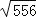 ≈ .
≈ . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式中是完全平方式的是( )
A. 2x2+4x-4 B. 16x2-8y2+1 C. 9a2-12a+4 D. x2y2+2xy+y2
相关试题

