【题目】解答
(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD.
∠BAD.
求证:EF=BE+FD;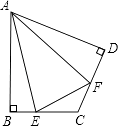
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是边BC,CD上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立? 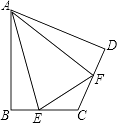
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF= ![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明. 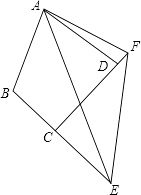
参考答案:
【答案】
(1)证明:延长EB到G,使BG=DF,连接AG.
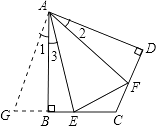
∵∠ABG=∠ABC=∠D=90°,AB=AD,
∴△ABG≌△ADF.
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF= ![]() ∠BAD.
∠BAD.
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD
(2)解:(1)中的结论EF=BE+FD仍然成立
(3)证明:结论EF=BE+FD不成立,应当是EF=BE﹣FD.
证明:在BE上截取BG,使BG=DF,连接AG.
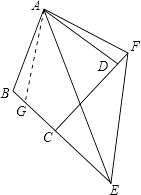
∵∠B+∠ADC=180°,∠ADF+∠ADC=180°,
∴∠B=∠ADF.
∵AB=AD,
∴△ABG≌△ADF.
∴∠BAG=∠DAF,AG=AF.
∴∠BAG+∠EAD=∠DAF+∠EAD
=∠EAF= ![]() ∠BAD.
∠BAD.
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF.
∴EG=EF
∵EG=BE﹣BG
∴EF=BE﹣FD
【解析】(1)可通过构建全等三角形来实现线段间的转换.延长EB到G,使BG=DF,连接AG.目的就是要证明三角形AGE和三角形AEF全等将EF转换成GE,那么这样EF=BE+DF了,于是证明两组三角形全等就是解题的关键.三角形ABE和AEF中,只有一条公共边AE,我们就要通过其他的全等三角形来实现,在三角形ABG和AFD中,已知了一组直角,BG=DF,AB=AD,因此两三角形全等,那么AG=AF,∠1=∠2,那么∠1+∠3=∠2+∠3=∠EAF= ![]() ∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.(2)思路和作辅助线的方法与(1)完全一样,只不过证明三角形ABG和ADF全等中,证明∠ABG=∠ADF时,用到的等角的补角相等,其他的都一样.因此与(1)的结果完全一样.(3)按照(1)的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使BG=DF,连接AG.根据(1)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE﹣BG=BE﹣DF.所以(1)的结论在(3)的条件下是不成立的.
∠BAD.由此就构成了三角形ABE和AEF全等的所有条件(SAS),那么就能得出EF=GE了.(2)思路和作辅助线的方法与(1)完全一样,只不过证明三角形ABG和ADF全等中,证明∠ABG=∠ADF时,用到的等角的补角相等,其他的都一样.因此与(1)的结果完全一样.(3)按照(1)的思路,我们应该通过全等三角形来实现相等线段的转换.就应该在BE上截取BG,使BG=DF,连接AG.根据(1)的证法,我们可得出DF=BG,GE=EF,那么EF=GE=BE﹣BG=BE﹣DF.所以(1)的结论在(3)的条件下是不成立的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于圆的周长公式C=2πR,下列说法正确的是( )
A. π、R是变量,2是常量 B. R是变量,π是常量
C. C是变量,π、R是常量 D. C、R是变量,2、π是常量
-
科目: 来源: 题型:
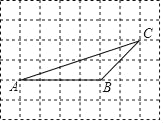
查看答案和解析>>【题目】如图,在方格纸中,点A、B、C是三个格点(网格线的交点叫做格点)
(1)过点C画AB的垂线,垂足为D;
(2)将点D沿BC翻折,得到点E,作直线CE;
(3)直线CE与直线AB的位置关系是 ;
(4)判断:∠ACB ∠ACE.(填“>”、“<”或“=”
-
科目: 来源: 题型:
查看答案和解析>>【题目】某射击运动员在相同条件下的射击160次,其成绩记录如下:
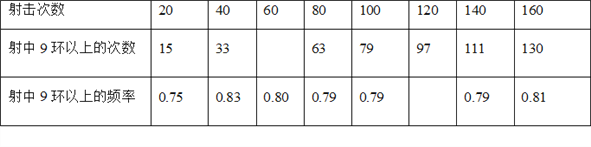
(1)根据上表中的信息将两个空格的数据补全(射中9环以上的次数为整数,频率精确到0.01);
(2)根据频率的稳定性,估计这名运动员射击一次时“射中9环以上”的概率(精确到0.1),
并简述理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用四舍五入法对0.02015(精确到千分位)取近似数是( )
A.0.02
B.0.020
C.0.0201
D.0.0202 -
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明命题“三角形中最多有一个角是直角”时,下列假设正确的是( )
A.三角形中最少有一个角是直角
B.三角形中没有一个角是直角
C.三角形中三个角全是直角
D.三角形中有两个或三个角是直角
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣(x﹣1)2+3,当t<x<4时,y随x的增大而减小,则实数t的取值范围是( )
A.t<0B.0≤t<1C.1≤t<4D.t≥4
相关试题

