【题目】如图,在△ABC中,DE是边AB的垂直平分线,交AB于E、交AC于D,连接BD. 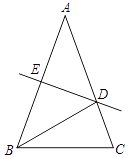
(1)若∠ABC=∠C,∠A=40°,求∠DBC的度数;
(2)若AB=AC,且△BCD的周长为18cm,△ABC的周长为30cm,求BE的长.
参考答案:
【答案】
(1)解:∵∠ABC=∠C,∠A=40°,
∴∠ABC=(180°﹣40°)÷2=70°.
∵DE是边AB的垂直平分线,
∴AD=DB,
∴∠ABD=∠A=40°,
∴∠DBC=∠ABC﹣∠ABD=70°﹣40°=30°
(2)解:∵DE是边AB的垂直平分线,
∴AD=DB,AE=BE,
∵△BCD的周长为18cm,
∴AC+BC=AD+DC+BC=DB+DC+BC=18cm.
∵△ABC的周长为30cm,
∴AB=30﹣(AC+BC)=30﹣18=12cm,
∴BE=12÷2=6cm
【解析】(1)首先计算出∠ABC的度数,再根据线段垂直平分线上任意一点,到线段两端点的距离相等可得AD=BD,进而可得∠ABD=∠A=40°,然后可得答案;(2)根据线段垂直平分线的性质可得AD=DB,AE=BE,然后再计算出AC+BC的长,再利用△ABC的周长为30cm可得AB长,进而可得答案.
【考点精析】关于本题考查的三角形的内角和外角和线段垂直平分线的性质,需要了解三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x+1)(2x-3)的结果为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x-3y)2=(x+3y)2+M,则M=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程(m﹣1)x2+2x+m2﹣1=0的常数项为0,则m的值是( )
A. 1B. ±1C. ﹣1D. ±2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,与2a的同类项的是( )
A.3a
B.2ab
C.﹣3a2
D.a2b -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,AB=AC,D是AB上一点,DE⊥BC于点E,ED的延长线交CA的延长线于点F.求证:△ADF是等腰三角形.
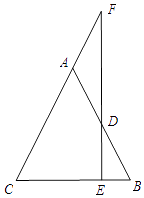
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是有理数,若a在数轴上的对应点的位置如图所示,a+b<0,有以下结论: ①b<0;②b﹣a>0;③|﹣a|>﹣b;④
 .
.
则所有正确的结论是( )
A.①,④
B.①,③
C.②,③
D.②,④
相关试题

