【题目】已知关于x的一次函数y=(2m-4)x+3n.
(1)当m,n取何值时,y随x的增大而增大?
(2)当m,n取何值时,函数图象经过原点?
(3)当m,n取何值时,函数图象与y轴交点在x轴上方?
(4)若图象经过一、三、四象限,求m,n的取值范围?
参考答案:
【答案】(1)m>2,n为全体实数;(2)m≠2,n=0,(3)n>0,m≠2,(4)m>2,n<0.
【解析】试题分析:
(1)由一次函数y=(2m-4)x+3n中y随x的增大而增大可得:2m-4>0,3n为任意实数即可求得对应的m、n的取值范围;
(2)由一次函数y=(2m-4)x+3n的图象过原点可得:2m-4![]() 0,3n=0,由此即可求得对应的m、n的取值范围;
0,3n=0,由此即可求得对应的m、n的取值范围;
(3)由一次函数y=(2m-4)x+3n的图象与y轴的交点在x轴上方可得:2m-4![]() 0,3n>0,由此即可解得对应的m,n的取值范围;
0,3n>0,由此即可解得对应的m,n的取值范围;
(4)由一次函数y=(2m-4)x+3n的图象过第一、三、四象限可得:2m-4>0,3n<0,由此即可求得对应的m,n的取值范围.
试题解析:
由题意可知:k=2m-4,b=3n,
(1)∵y随x的增大而增大,
∴k>0,b为任意实数,
∴2m-4>0,3n为任意实数,
∴m>2,n为全体实数;
(2)∵函数图象经过原点,
∴k≠0,b=0,即2m-4≠0,3n=0,
∴m≠2,n=0;
(3)∵函数图象与y轴交点在x轴上方,
∴b>0,k≠0,即3n>0,2m-4≠0,
∴n>0,m≠2;
(4)∵图象经过一、三、四象限,求m,n的取值范围,
∴k>0,b<0,即2m-4>0,3n<0,
∴m>2,n<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个数中最小的数是( )
A.﹣1B.0C.2D.﹣(﹣1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2.5°=( )
A.15′B.25′C.150′D.250′
-
科目: 来源: 题型:
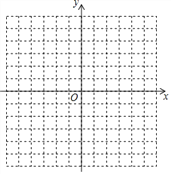
查看答案和解析>>【题目】(1)在如图所示的平面直角坐标系中表示下面各点:A(0,3);B(5,0);C(3,-5);D(-3,-5);E(3,5);
(2)连接CE,则直线CE与y轴是什么位置关系?
(3)点D分别到x、y轴的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形不正确的是( )
A.若x=y,则x+3=y+3B.若x=y,则x﹣3=y﹣3
C.若x=y,则﹣3x=﹣3yD.若x2=y2,则x=y
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
(1)求树DE的高度;
(2)求食堂MN的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
 (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE= .
.(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使
 ,求点P的坐标;
,求点P的坐标;(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.

相关试题

