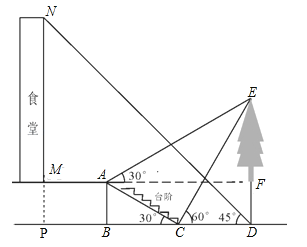
【题目】小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
(1)求树DE的高度;
(2)求食堂MN的高度.

参考答案:
【答案】(1)6;(2)![]() .
.
【解析】试题分析:(1)设DE=x,可得EF=DE﹣DF=x﹣2,从而得AF=![]() (x﹣2),再求出CD=
(x﹣2),再求出CD=![]() x、BC的长,根据AF=BD可得关于x的方程,解之可得;
x、BC的长,根据AF=BD可得关于x的方程,解之可得;
(2)延长NM交DB延长线于点P,知AM=BP=3,由(1)得CD=![]() x=
x=![]() 、BC=
、BC=![]() ,根据NP=PD且AB=MP可得答案.
,根据NP=PD且AB=MP可得答案.
试题解析:(1)如图,设DE=x,∵AB=DF=2,∴EF=DE﹣DF=x﹣2,∵∠EAF=30°,∴AF=![]() =
=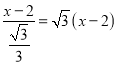 ,又∵CD=
,又∵CD=![]() =
=![]() =
=![]() x,BC=
x,BC=![]() =
=![]() =
=![]() ,∴BD=BC+CD=
,∴BD=BC+CD=![]() +
+![]() x,由AF=BD可得
x,由AF=BD可得![]() (x﹣2)=
(x﹣2)=![]() +
+![]() x,解得:x=6,∴树DE的高度为6米;
x,解得:x=6,∴树DE的高度为6米;
(2)延长NM交DB延长线于点P,则AM=BP=3,由(1)知CD=![]() x=
x=![]() ×6=
×6=![]() ,BC=
,BC=![]() ,∴PD=BP+BC+CD=3+
,∴PD=BP+BC+CD=3+![]() +
+![]() =3+
=3+![]() ,∵∠NDP=45°,且MP=AB=2,∴NP=PD=3+
,∵∠NDP=45°,且MP=AB=2,∴NP=PD=3+![]() ,∴NM=NP﹣MP=3+
,∴NM=NP﹣MP=3+![]() ﹣2=
﹣2=![]() ,∴食堂MN的高度为
,∴食堂MN的高度为![]() 米.
米.
-
科目: 来源: 题型:
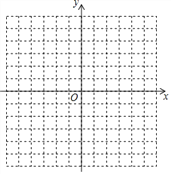
查看答案和解析>>【题目】(1)在如图所示的平面直角坐标系中表示下面各点:A(0,3);B(5,0);C(3,-5);D(-3,-5);E(3,5);
(2)连接CE,则直线CE与y轴是什么位置关系?
(3)点D分别到x、y轴的距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一次函数y=(2m-4)x+3n.
(1)当m,n取何值时,y随x的增大而增大?
(2)当m,n取何值时,函数图象经过原点?
(3)当m,n取何值时,函数图象与y轴交点在x轴上方?
(4)若图象经过一、三、四象限,求m,n的取值范围?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形不正确的是( )
A.若x=y,则x+3=y+3B.若x=y,则x﹣3=y﹣3
C.若x=y,则﹣3x=﹣3yD.若x2=y2,则x=y
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
 (a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE=
(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE= .
.(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使
 ,求点P的坐标;
,求点P的坐标;(4)在坐标轴上找一点M,使以点B、C、M为顶点的三角形与△ACD相似,直接写出点M的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=-x+m的图象和y轴交于点B,与正比例函数y=x图象交于点P (2,n).
(1)求m和n的值;
(2)求△POB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.



相关试题

