【题目】已知，抛物线（a＜0）与x轴交于A（3，0）、B两点，与y轴交于点C，抛物线的对称轴是直线x=1，D为抛物线的顶点，点E在y轴C点的上方，且CE=．

（1）求抛物线的解析式及顶点D的坐标；

（2）求证：直线DE是△ACD外接圆的切线；

（3）在直线AC上方的抛物线上找一点P，使，求点P的坐标；

（4）在坐标轴上找一点M，使以点B、C、M为顶点的三角形与△ACD相似，直接写出点M的坐标．

参考答案：

【答案】（1），顶点D（1，4）；（2）证明见解析；（3）P（， ）或（， ）；（4）（0，0）或（9，0）或（0，﹣）．

【解析】试题分析：（1）由对称轴求出B的坐标，由待定系数法求出抛物线解析式，即可得出顶点D的坐标；

（2）由勾股定理和勾股定理的逆定理证出△ACD为直角三角形，∠ACD=90°．得出AD为△ACD外接圆的直径，再证明△AED为直角三角形，∠ADE=90°．得出AD⊥DE，即可得出结论；

（3）求出直线AC的解析式，再求出线段AD的中点N的坐标，过点N作NP∥AC，交抛物线于点P，求出直线NP的解析式，与抛物线联立，即可得出答案；

（4）由相似三角形的性质和直角三角形的性质即可得出答案．

试题解析：（1）∵抛物线的对称轴是直线x=1，点A（3，0），∴根据抛物线的对称性知点B的坐标为（﹣1，0），OA=3，将A（3，0），B（﹣1，0）代入抛物线解析式中得： ，解得： ，∴抛物线解析式为；当x=1时，y=4，∴顶点D（1，4）．

（2）当=0时，∴点C的坐标为（0，3），∴AC= =，CD==，AD= =，∴AC2+CD2=AD2，∴△ACD为直角三角形，∠ACD=90°，∴AD为△ACD外接圆的直径，∵点E在 轴C点的上方，且CE=，∴E（0， ），∴AE= =，DE=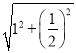 =，∴DE2+AD2=AE2，∴△AED为直角三角形，∠ADE=90°，∴AD⊥DE，又∵AD为△ACD外接圆的直径，∴DE是△ACD外接圆的切线；

（3）设直线AC的解析式为y=kx+b，根据题意得： ，解得： ，∴直线AC的解析式为y=﹣x+3，∵A（3，0），D（1，4），∴线段AD的中点N的坐标为（2，2），过点N作NP∥AC，交抛物线于点P，设直线NP的解析式为y=﹣x+c，则﹣2+c=2，解得：c=4，∴直线NP的解析式为y=﹣x+4，由y=﹣x+4，y=﹣x2+2x+3联立得：﹣x2+2x+3=﹣x+4，解得：x=或x=，∴y=，或y=，∴P（， ）或（， ）；

（4）分三种情况：①M恰好为原点，满足△CMB∽△ACD，M（0，0）；

②M在x轴正半轴上，△MCB∽△ACD，此时M（9，0）；

③M在y轴负半轴上，△CBM∽△ACD，此时M（0，﹣ ）；

综上所述，点M的坐标为（0，0）或（9，0）或（0，﹣ ）．

关闭