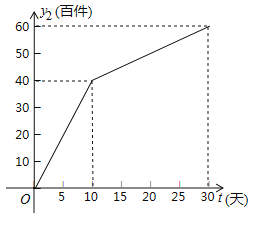
【题目】(2017湖北省荆门市)我市雷雷服饰有限公司生产了一款夏季服装,通过实体商店和网上商店两种途径进行销售,销售一段时间后,该公司对这种商品的销售情况,进行了为期30天的跟踪调查,其中实体商店的日销售量y1(百件)与时间t(t为整数,单位:天)的部分对应值如下表所示,网上商店的日销售量y2(百件)与时间t(t为整数,单位:天)的部分对应值如图所示.
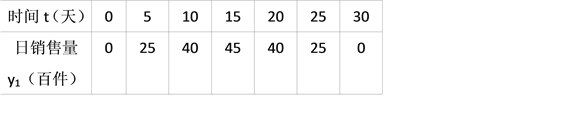
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数能反映y1与t的变化规律,并求出y1与t的函数关系式及自变量t的取值范围;
(2)求y2与t的函数关系式,并写出自变量t的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为y(百件),求y与t的函数关系式;当t为何值时,日销售总量y达到最大,并求出此时的最大值.
参考答案:
【答案】(1)![]() (0≤t≤30,且为整数);(2)
(0≤t≤30,且为整数);(2) ;(3)
;(3) ,当t=17或18时,y最大=91.2百件.
,当t=17或18时,y最大=91.2百件.
【解析】试题分析:(1)根据观察可设y1=at2+bt+c,将(0,0),(5,25),(10,40)代入即可得到结论;
(2)当0≤t≤10时,设y2=kt,求得y2与t的函数关系式为:y2=4t,当10≤t≤30时,设y2=mt+n,将(10,40),(30,60)代入得到y2与t的函数关系式为:y2=k+30,(3)依题意得y=y1+y2,当0≤t≤10时,得到y最大=80;当10<t≤30时,得到y最大=91.2,于是得到结论.
试题解析:解(1)根据观察可设![]() ,将(0,0),(5,25),(10,40)代入得:
,将(0,0),(5,25),(10,40)代入得:  ,解得:
,解得:  ,∴y1与t的函数关系式为:
,∴y1与t的函数关系式为: ![]() (0≤t≤30,且为整数);
(0≤t≤30,且为整数);
(2)当0≤t≤10时,设y2=kt,∵(10,40)在其图象上,∴10k=40,∴k=4,∴y2与t的函数关系式为:y2=4t,当10≤t≤30时,设y2=mt+n,将(10,40),(30,60)代入得: ![]() ,解得:
,解得: ![]() ,∴y2与t的函数关系式为:y2=t+30,综上所述,
,∴y2与t的函数关系式为:y2=t+30,综上所述,  ;
;
(3)依题意得y=y1+y2,当0≤t≤10时,y=![]() =
=![]() =
=![]() (t﹣25)2+125,∴t=10时,y最大=80;
(t﹣25)2+125,∴t=10时,y最大=80;
当10<t≤30时,y=![]() t2+6t+t+30=
t2+6t+t+30=![]() =
=![]() ,∵t为整数,∴t=17或18时,y最大=91.2,∵91.2>80,∴当t=17或18时,y最大=91.2(百件).
,∵t为整数,∴t=17或18时,y最大=91.2,∵91.2>80,∴当t=17或18时,y最大=91.2(百件).
综上所述:  ,当t=17或18时,y最大=91.2百件.
,当t=17或18时,y最大=91.2百件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,
 是坐标原点,点A(2,5)在反比例函数
是坐标原点,点A(2,5)在反比例函数 的图象上.一次函数
的图象上.一次函数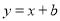 的图象过点A,且与反比例函数图象的另一交点为B.
的图象过点A,且与反比例函数图象的另一交点为B.(1)求
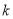 和
和 的值;
的值; (2)设反比例函数值为
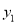 ,一次函数值为
,一次函数值为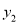 ,求
,求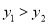 时
时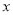 的取值范围.
的取值范围.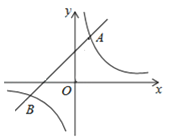
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数
 ,
, ,
, 在数轴上的位置如下图所示:
在数轴上的位置如下图所示:
(1)若
 ,求
,求 的值.
的值.(2)若
 ,
, ,
, ,且
,且 ,
, ,
, 对应的点分别为
对应的点分别为 ,
, ,
, ,问在数轴上是否存在一点
,问在数轴上是否存在一点 ,使
,使 与
与 的距离是
的距离是 与
与 的距离的3倍.若存在,请求出
的距离的3倍.若存在,请求出 点对应的有理数;若不存在,请说明理由.
点对应的有理数;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)用含a的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的
 ,求出此时通道的宽.
,求出此时通道的宽.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只甲虫在5×5的方格(每小格边长为1个单位长度)上沿着网格线运动,它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B记为:A→B(+1,+4),从D到C记为:D→C(-1,+2)第一个数表示左右方向,第二个数表示上下方向.
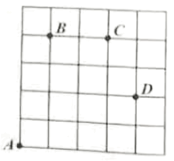
(1)图中A→C可以记为( , )
(2)图中D→ 可以记为(-4,-2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)2014年益阳市的地区生产总值(第一、二、三产业的增加值之和)已进入千亿元俱乐部,如图表示2014年益阳市第一、二、三产业增加值的部分情况,请根据图中提供的信息解答下列问题

(1)2014年益阳市的地区生产总值为多少亿元?
(2)请将条形统计图中第二产业部分补充完整;
(3)求扇形统计图中第二产业对应的扇形的圆心角度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

相关试题

