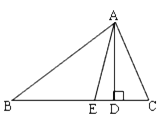
【题目】如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
(1)若∠B=40°,∠C=70°,求∠DAE的度数,并说明理由;
(2)若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系 .(不需说明理由)
参考答案:
【答案】(1)15°;(2)![]()
【解析】
(1)利用三角形的内角和定理求出∠BAC,再利用角平分线定义求∠BAD,最后求出∠DAE的度数,即可解答;
(2)根据三角形内角和等于180°,所以∠BAC=180°-∠B-∠C,因为AE平分∠BAC,利用∠BAD=90°-∠B,可得结论.
解:(1)∵∠C=70°,∠B=40°,
∴∠BAC=180°-(∠B+∠C)=180°-40°-70°=70°,
∵AE平分∠BAC,
∴∠CAE=![]() ∠BAC=35°
∠BAC=35°
∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=90°-70°=20°,
∴∠DAE=∠CAE-∠CAD=35°-20°=15°;
(2) ![]() ,
,
理由:∵AE为角平分线,
∴∠BAE=![]() ,
,
∵AD⊥BC,
∴∠BAD=90°-∠B,
∴∠DAE=∠BAD-∠BAE
=90°-∠B-![]()
==![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:

(1)△AEH≌△CGF;
(2)四边形EFGH是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】本学期开学前夕,苏州某文具店用4000元购进若干书包,很快售完,接着又用4500元购进第二批书包,已知第二批所购进书包的只数是第一批所购进书包的只数的1.5倍,且每只书包的进价比第一批的进价少5元,求第一批书包每只的进价是多少?
-
科目: 来源: 题型:
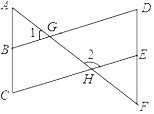
查看答案和解析>>【题目】如图,已知AF分别与BD、CE交于点G、H,∠1=50°,∠2=130°.
(1)BD与CE平行吗?为什么?
(2)若∠A=∠F,探索∠C与∠D的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABD和△ACE分别是等边三角形,AB≠AC,下列结论中正确有( )个.(1)DC=BE,(2)∠BOD=60°,(3)∠BDO=∠CEO,(4)AO平分∠DOE,(5)AO平分∠BAC.
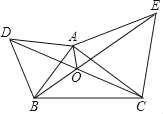
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图1中的三角板OMN绕点O按逆时针方向旋转,使∠BON=30°,如图2,MN与CD相交于点E,求∠CEN的度数;
(2)将图1中的三角尺OMN绕点O按每秒20°的速度沿逆时针方向旋转一周,在旋转的过程中,求在第几秒时,边MN恰好与边CD平行?(友情提醒:先画出符合题意的图形,然后再探究)
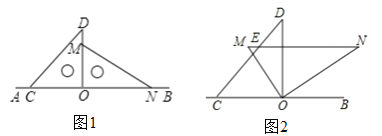
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.

相关试题

