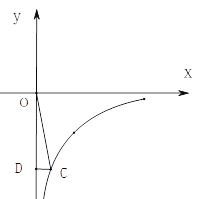
【题目】如图,点C在反比例函数y=![]() 的图象上,过点C作CD⊥y轴,交y轴负半轴于点D,且△ODC的面积是3.
的图象上,过点C作CD⊥y轴,交y轴负半轴于点D,且△ODC的面积是3.
(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)若CD=1,求直线OC的解析式.
参考答案:
【答案】(1)y=![]() (2)y=﹣6x
(2)y=﹣6x
【解析】试题分析:(1)设C点坐标为(x,y),根据k的几何意义得到|k|=2×3=6,而图象在第四象限,则k=﹣6;
(2)由于CD=1,则点C ( 1,y ),利用反比例函数解析式确定C点坐标,然后根据待定系数法求直线OC的解析式.
试题解析:解:(1)设C点坐标为(x,y).∵△ODC的面积是3,∴ ![]() ODDC=
ODDC=![]() x(﹣y)=3,∴xy=﹣6,而xy=k,∴k=﹣6,∴所求反比例函数解析式为
x(﹣y)=3,∴xy=﹣6,而xy=k,∴k=﹣6,∴所求反比例函数解析式为![]() ;
;
(2)∵CD=1,即点C ( 1,y ),把x=1代入![]() ,得y=﹣6,∴C 点坐标为(1,﹣6),设直线OC的解析式为y=mx,把C (1,﹣6)代入y=mx得﹣6=m,∴直线OC的解析式为:y=﹣6x.
,得y=﹣6,∴C 点坐标为(1,﹣6),设直线OC的解析式为y=mx,把C (1,﹣6)代入y=mx得﹣6=m,∴直线OC的解析式为:y=﹣6x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=
 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).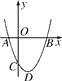
-
科目: 来源: 题型:
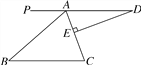
查看答案和解析>>【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,BC是⊙O的直径,∠ABC=30°,过点B作⊙O的切线BD,与CA的延长线交于点D,与半径AO的延长线交于点E,过点A作⊙O的切线AF,与直径BC的延长线交于点F.
(1)求证:△ACF∽△DAE;
(2)若S△AOC=
 ,求DE的长;
,求DE的长;(3)连接EF,求证:EF是⊙O的切线.

【答案】(1) 见解析; (2)3
 ;(3)见解析.
;(3)见解析.【解析】试题分析:(1)根据圆周角定理得到∠BAC=90°,根据三角形的内角和得到∠ACB=60°根据切线的性质得到∠OAF=90°,∠DBC=90°,于是得到∠D=∠AFC=30°由相似三角形的判定定理即可得到结论;
(2)根据S△AOC=
 ,得到S△ACF=
,得到S△ACF= ,通过△ACF∽△DAE,求得S△DAE=
,通过△ACF∽△DAE,求得S△DAE= ,过A作AH⊥DE于H,解直角三角形得到AH=
,过A作AH⊥DE于H,解直角三角形得到AH= DH=
DH= DE,由三角形的面积公式列方程即可得到结论;
DE,由三角形的面积公式列方程即可得到结论;(3)根据全等三角形的性质得到OE=OF,根据等腰三角形的性质得到∠OFG=
 (180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.
(180°﹣∠EOF)=30°,于是得到∠AFO=∠GFO,过O作OG⊥EF于G,根据全等三角形的性质得到OG=OA,即可得到结论.试题解析:(1)证明:∵BC是⊙O的直径,∴∠BAC=90°,∵∠ABC=30°,∴∠ACB=60°
∵OA=OC,∴∠AOC=60°,∵AF是⊙O的切线,∴∠OAF=90°,∴∠AFC=30°,∵DE是⊙O的切线,∴∠DBC=90°,∴∠D=∠AFC=30,∵∠DAE=ACF=120°,∴△ACF∽△DAE;
(2)∵∠ACO=∠AFC+∠CAF=30°+∠CAF=60°,∴∠CAF=30°,∴∠CAF=∠AFC,∴AC=CF,∴OC=CF,∵S△AOC=
 ,∴S△ACF=
,∴S△ACF= ,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB=
,∵∠ABC=∠AFC=30°,∴AB=AF,∵AB= BD,∴AF=
BD,∴AF= BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴
BD,∴∠BAE=∠BEA=30°,∴AB=BE=AF,∴ ,∵△ACF∽△DAE,∴
,∵△ACF∽△DAE,∴ =
= ,∴S△DAE=
,∴S△DAE= ,过A作AH⊥DE于H,∴AH=
,过A作AH⊥DE于H,∴AH= DH=
DH= DE,∴S△ADE=
DE,∴S△ADE= DEAH=
DEAH= ×
×
 =
= ,∴DE=
,∴DE=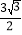 ;
;(3)∵∠EOF=∠AOB=120°,∴∠OEB=∠AFO,在△AOF与△BOE中,∵∠OBE=∠OAF,∠OEB=∠AFO,OA=OB,∴△AOF≌△BEO,∴OE=OF,∴∠OFG=
 (180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.
(180°﹣∠EOF)=30°,∴∠AFO=∠GFO,过O作OG⊥EF于G,∴∠OAF=∠OGF=90°,在△AOF与△OGF中,∵∠OAF=∠OGF,∠AFO=∠GFO,OF=OF,∴△AOF≌△GOF,∴OG=OA,∴EF是⊙O的切线.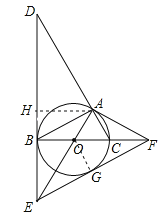
【题型】解答题
【结束】
25【题目】如图,在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A,C的坐标分别是A(0,2)和C(2
 ,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.
,0),点D是对角线AC上一动点(不与A,C重合),连结BD,作DE⊥DB,交x轴于点E,以线段DE,DB为邻边作矩形BDEF.(1)填空:点B的坐标为 ;
(2)是否存在这样的点D,使得△DEC是等腰三角形?若存在,请求出AD的长度;若不存在,请说明理由;
(3)①求证:
 ;
;②设AD=x,矩形BDEF的面积为y,求y关于x的函数关系式(可利用①的结论),并求出y的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店分两次购进
 、
、 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
(1)求
 、
、 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?(2)商场决定
 商品以每件
商品以每件 元出售,
元出售, 商品以每件
商品以每件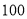 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进 、
、 两种商品共
两种商品共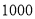 件,且
件,且 商品的数量不少于
商品的数量不少于 种商品数量的
种商品数量的 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润. -
科目: 来源: 题型:
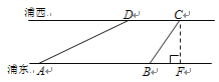
查看答案和解析>>【题目】如图,世博园段的浦江两岸互相平行,C、D是浦西江边间隔200m的两个场馆.海宝在浦东江边的宝钢大舞台A处,测得∠DAB=30°, 然后沿江边走了500m到达世博文化中心B处,测得∠CBF=60°, 求世博园段黄浦江的宽度(结果可保留根号).
相关试题

