【题目】综合与实践
阅读以下材料:
定义:两边分别相等且夹角互补的两个三角形叫做“互补三角形”.
用符号语言表示为:如图①,在△ABC与△DEF中,如果AC=DE,∠C+∠E=180°,BC=EF,那么△ABC与△DEF是互补三角形.
反之,“如果△ABC与△DEF是互补三角形,那么有AC=DE,∠C+∠E=180°,BC=EF”也是成立的.
自主探究
利用上面所学知识以及全等三角形的相关知识解决问题:
(1)性质:互补三角形的面积相等
如图②,已知△ABC与△DEF是互补三角形.
求证:△ABC与△DEF的面积相等.
证明:分别作△ABC与△DEF的边BC,EF上的高线,则∠AGC=∠DHE=90°.
…… (将剩余证明过程补充完整)
(2)互补三角形一定不全等,请你判断该说法是否正确,并说明理由,如果不正确,请举出一个反例,画出示意图.

参考答案:
【答案】(1)见解析;(2)不正确,理由见解析
【解析】
(1)已知△ABC与△DEF是互补三角形,可得∠ACB+∠E=180°,AC=DE,BC=EF,证得∠ACG=∠E,证明△AGC≌△DHE,得到AG=DH,所以![]() ,即△ABC与△DEF的面积相等.
,即△ABC与△DEF的面积相等.
(2)不正确.先画出反例图,证明△ABC≌△DEF,△ABC与△DEF是互补三角形.互补三角形一定不全等的说法错误.
(1)∵△ABC与△DEF是互补三角形,
∴∠ACB+∠E=180°,AC=DE,BC=EF.
又∵∠ACB+∠ACG=180°,
∴∠ACG=∠E,
在△AGC与△DHE中,

∴△AGC≌△DHE(AAS)
∴AG=DH.
∴![]()
即△ABC与△DEF的面积相等.
(2)不正确.
反例如解图,在△ABC和△DEF中,

∴△ABC≌△DEF(SAS),
∴△ABC与△DEF是互补三角形.
∴互补三角形一定不全等的说法错误.

-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象过A(﹣3,0),B(1,0),C(0,3),点D在函数图象上,点C,D是二次函数图象上的一对对称点,一次函数图象过点B,D,求:
(1)一次函数和二次函数的解析式;
(2)写出使一次函数值大于二次函数值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+3x+4与x轴交于点A,B,与y轴交于点C,P(m,n)为第一象限内抛物线上的一点,点D的坐标为(0,6).

(1)OB=_________,抛物线的顶点坐标为_________________;
(2)当n=4时,求点P关于直线BC的对称点P′的坐标;
(3)是否存在直线PD,使直线PD所对应的一次函数随x的增大而增大?若存在,直接写出m的取值范围;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果
 ,且
,且 .下列说法中,正确的个数是( )
.下列说法中,正确的个数是( )①
 ; ②如果
; ②如果 ,那么
,那么 ;③
;③ ; ④
; ④
A.
 个B.
个B.  个C.
个C. 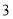 个D.
个D.  个
个 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
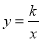 与
与 (
(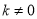 )在同一直角坐标系中的大致图象可能是( )
)在同一直角坐标系中的大致图象可能是( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

