【题目】如图,在等边三角形ABC中,顶点A,C处各有一只蚂蚁,它们同时出发,分别以同样的速度由A向B和由C向A爬行,经过t秒后,它们分别到达D,E处,请问两只蚂蚁在爬行过程中,
(1)CD与BE有何数量关系,为什么?
(2)DC与BE相交所成的∠BFC的大小是否发生变化?若有变化,请说明理由;若没有变化,求出∠BFC的大小。

参考答案:
【答案】(1)CD=BE,理由见解析;(2)∠BFC的大小不变,始终为120°
【解析】试题分析:(1)证明△ACD≌△CBE即可证明CD=BE;(2)要求∠BFC的度数即要求∠FBC和∠FCB的和,即要求∠FCB和∠ACD的度数之和,即为∠ACB的度数,为60°,因此可得出∠BFC=120°,保持不变.
试题解析:
(1)CD=BE,
∵两只蚂蚁同时出发,同样的速度,
∴AD=CE,
又 ∵△ABC是等边三角形,
∴AC=BC ,∠A=∠BCE=60°,
∵在△ACD和△CBE中
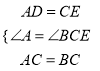 ,
,
∴△ACD≌△CBE (SAS),
∴CD=BE;
(2)∠BFC 大小不会发生变化,
∵△ACD≌△CBE,
∴∠DCA=∠EBC,
又∵∠DCA+∠DCB=60°,
∴∠EBC+∠DCB=60°,
∴∠BFC=180°-60°=120°,
∴∠BFC的大小不变,始终为120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形三边a,b,c满足(a+b)2=c2+2ab,则这个三角形是( )
A. 等边三角形 B. 钝角三角形 C. 等腰直角三角形 D. 直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个漂亮的礼物盒是一个有11个面的棱柱,那么它有_____个顶点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
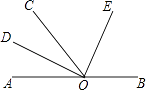
(1)∠AOD的余角是 , ∠COD的余角是
(2)OE是∠BOC的平分线吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】折叠一张正方形纸片,按如下折法不一定能折出45°角的是( )
A.
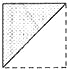 B.
B.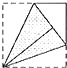 C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于下列各组条件,不能判定△
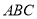 ≌△
≌△ 的一组是 ( )
的一组是 ( )A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆大堂有6 根圆柱形大柱,高10 米,大柱周长25.12 分米,要全部涂上油漆,如果按每平方米的油漆费为80 元计算,需用多少钱?
相关试题

