【题目】矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为cm2 .
参考答案:
【答案】4或12
【解析】解:本题有两种情况, 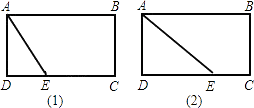
⑴DE=1cm,EC=3cm.因为AE平分∠DAB,
故∠DAE=45°,△ADE中,AD=DE=1,
矩形面积为1×(1+3)=4cm2.(2)DE=3cm,EC=1cm.因为AE平分∠DAB,
故∠DAE=45°,△ADE中,AD=DE=3,
矩形面积为3×(1+3)=12cm2.
所以答案是4或12.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的周长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为2,H在CD的延长线上,四边形CEFH也为正方形,则△DBF的面积为 .
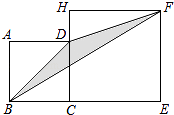
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB. 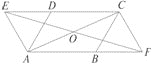
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
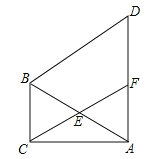
-
科目: 来源: 题型:
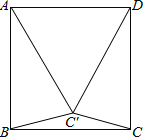
查看答案和解析>>【题目】如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A.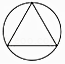
B.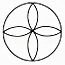
C.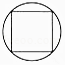
D.
相关试题

