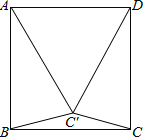
【题目】如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.
参考答案:
【答案】△DCC′,△DC′A,△C′AB,△C′BC,理由见解析.
【解析】
试题利用旋转的性质以及正方形的性质进而得出等腰三角形,再利用全等三角形的判定与性质判断得出.
试题解析:图中的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,理由如下:
∵四边形ABCD是正方形,∴AB=AD=DC,∠BAD=∠ADC=90°.∴DC=DC′=DA.
∴△DCC′,△DC′A为等腰三角形.
∵∠C′DC=30°,∠ADC=90°,∴∠ADC′=60°.∴△AC′D为等边三角形.
∵∠C′AB=90°-60°=30°,∴∠CDC′=∠C′AB.
在△DCC′和△AC′B中CD=BA,∠CDC′=∠C′AB,C′D=C′A,
∴△DCC′≌△AC′B(SAS).∴CC′=C′B,∴△BCC′为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB. 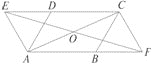
(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为cm2 .
-
科目: 来源: 题型:
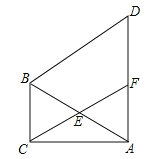
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
(1)求证:四边形BCFD为平行四边形;
(2)若AB=6,求平行四边形BCFD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
A.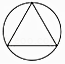
B.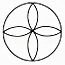
C.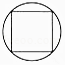
D.
-
科目: 来源: 题型:
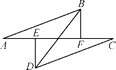
查看答案和解析>>【题目】如图,点A,E,F,C在一条直线上,若将△DEC的边EC沿AC方向平移,平移过程中始终满足下列条件:AE=CF,DE⊥AC于点E,BF⊥AC于点F,且AB=CD.则当点E,F不重合时,BD与EF的关系是______.
-
科目: 来源: 题型:
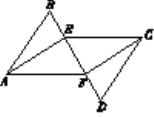
查看答案和解析>>【题目】如图,AB∥CD,AB=CD,点B、E、F、D在同一条直线上,∠BAE=∠DCF.
(1)求证:AE=CF;
(2)连结AF、EC,试猜想四边形AECF是什么四边形,并证明你的结论.
相关试题

