【题目】如图,在△ABC中∠BAC=120°,AB=AC,点M、N在边BC上,且∠MAN=60°若BM=2,CN=3,则MN的长为_______.

参考答案:
【答案】![]()
【解析】
利用旋转作△APC,连接PN,根据旋转得:△ABM≌△ACP,PC=BM=2,证明△MAN≌△PAN,则MN=PN,作高线PD,利用勾股定理计算PD和PN的长,可得结论.
如图,△ABM绕点A逆时针旋转120°至△APC,连接PN,过点P作BC的垂线,垂足为D,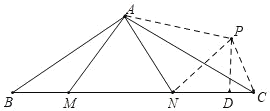
∵∠BAC=120°,AB=AC,
∴∠B=∠ACB=30°,
由旋转可得△ABM≌△APC,
∴∠B=∠ACP=30°,PC=BM=2,∠BAM=∠CAP,
∴∠NCP=60°,
∵∠MAN=60°,
∴∠BAM+∠NAC=∠NAC+∠CAP=60°=∠MAN,
又∵AM=AP,AN=AN,
∴△MAN≌△PAN(SAS),
∴MN=PN,
∵PD⊥CN,∠NCP=60°
∴![]() ,
,![]()
∴DN=CN-CD=3-1=2,
∴![]()
∴MN=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF.
(1)求△ABE的面积.
(2)求折痕EF的长.

-
科目: 来源: 题型:
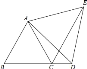
查看答案和解析>>【题目】如图,已知等边△ABC中,点D在BC边的延长线上,CE平分∠ACD,且CE=BD.判断△ADE的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,四边形ABCD为正方形,点E,F分别在AB与BC上,且∠EDF=45°,易证:AE+CF=EF(不用证明).
(1)如图②,在四边形ABCD中,∠ADC=120°,DA=DC,∠DAB=∠BCD=90°,点E,F分别在AB与BC上,且∠EDF=60°.猜想AE,CF与EF之间的数量关系,并证明你的猜想;
(2)如图③,在四边形ABCD中,∠ADC=2α,DA=DC,∠DAB与∠BCD互补,点E,F分别在AB与BC上,且∠EDF=α,请直接写出AE,CF与EF之间的数量关系,不用证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:身高在选定标准的±2%范围之内都称为“普通身高”.为了解某校九年级男生中具有“普通身高”的人数,我们从该校九年级500名男生中随机选出10名男生,分别测量出他们的身高(单位:cm)收集并整理统计表:
男生序号
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
身高
163
171
173
159
161
174
164
166
169
164
根据以上表格信息,解答如下问题:
(1)计算这组数据的三个统计量:平均数、中位数、众数;
(2)请你选择其中一个统计量作为选定标准,估计该校九年级男生中具有“普通身高”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=
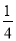 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC,△DEC均为直角三角形,B,C,E三点在一条直线上,过D作DM⊥AC于M.

(1)如图1,若△ABC≌△DEC,且AB=2BC.
①过B作BN⊥AC于N,则线段AN,BN,MN之间的数量关系为: ;(直接写出答案)
②连接ME,求
 的值;
的值; (2)如图2,若AB=CE=DE,DM=2,MC=1,求ME的长.
相关试题

