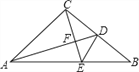
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过点C作AD的垂线,交AB于点F,求证∠ADC=∠BDE
参考答案:
【答案】见解析
【解析】试题分析:作CH⊥AB于H交AD于P,根据已知条件和等腰直角三角形的性质易证△APH≌△CEH,可得PH=EH,再证得CP=EB,∠PCD=∠EBD=45°,DC=DB,即可得△PDC≌△EDB,结论得证.
试题解析:
作CH⊥AB于H交AD于P,
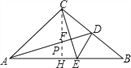
∵在Rt△ABC中,AC=CB,∠ACB=90°,
∴∠CAB=∠CBA=45.
∴∠HCB=90∠CBA=45=∠CBA.
又∵BC中点为D,
∴CD=BD.
又∵CH⊥AB,
∴CH=AH=BH.
又∵∠PAH+∠APH=90,∠PCF+∠CPF=90,∠APH=∠CPF,
∴∠PAH=∠ECH.
在△APH与△CEH中
∠PAH=∠ECH,AH=CH,∠PHA=∠EHC,
∴△APH≌△CEH(ASA).
∴PH=EH,
又∵PC=CHPH,BE=BHHE,
∴CP=EB.
∵△ACB是等腰直角三角形,
∴∠B=45,
即∠EBD=45,
∵CH⊥AB,
∴∠PCD=45=∠EBD,
在△PDC与△EDB中
PC=EB,∠PCD=∠EBD,DC=DB,
∴△PDC≌△EDB(SAS).
∴∠ADC=∠BDE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一个平面去截一个正方体,截面不可能是( )
A.梯形
B.五边形
C.六边形
D.圆 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,AD∥BC,∠ABC=90o,AB=BC,点E是AB上的点,∠ECD=45o,连接ED,过D作DF⊥BC于F.

(1)若∠BEC=75o,FC=4,求梯形ABCD的周长。(4分)
(2)求证:ED=BE+FC.(6分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x-2的平方根是±2 , y+7的立方根是2,求x+y的值.
-
科目: 来源: 题型:
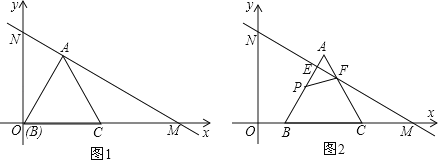
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,直线MN分别与x轴正半轴、y轴正半轴交于点M、N,且OM=6cm,∠OMN=30°,等边△ABC的顶点B与原点O重合,BC边落在x轴的正半轴上,点A恰好落在线段MN上,如图2,将等边△ABC从图1的位置沿x轴正方向以1cm/s的速度平移,边AB、AC分别与线段MN交于点E、F,在△ABC平移的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿折线B→A→C运动,当点P达到点C时,点P停止运动,△ABC也随之停止平移.设△ABC平移时间为t(s),△PEF的面积为S(cm2).
(1)求等边△ABC的边长;
(2)当点P在线段BA上运动时,求S与t的函数关系式,并写出自变量t的取值范围;
(3)点P沿折线B→A→C运动的过程中,是否在某一时刻,使△PEF为等腰三角形?若存在,求出此时t值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,不正确的是( )
A.零是整数
B.零没有倒数
C.零是最小的数
D.-1是最大的负整数
相关试题

