【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:今有甲种袋子中装有黄金9枚(每枚黄金重量相同),乙种袋子中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲种袋子比乙种袋子轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,则可建立方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
参考答案:
【答案】C
【解析】
设每枚黄金重x两,每枚白银重y两,根据“黄金9枚和白银11枚的重量相等,黄金8枚和白银1枚的重量比黄金1枚白银10枚轻13两”,即可得出关于x,y的二元一次方程,此题得解.
解:设每枚黄金重x两,每枚白银重y两,
依题意,得:![]()
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在网格中,每个小正方形的边长均为1个单位长度,我们将小正方形的顶点叫做格点,线段AB的端点均在格点上.
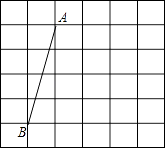
(1)将线段AB向右平移3个单位长度,得到线段A′B′,画出平移后的线段并连接AB′和A′B,两线段相交于点O;
(2)求证:△AOB≌△B′OA′. -
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究及应用.

(1)如图 1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式)
(3)比较图 1,图 2 的阴影部分面积,可以得到乘法公式 (用式子表达)
(4)应用所得的公式计算:(1﹣
 )(1﹣
)(1﹣ )(1﹣
)(1﹣ )…(1﹣
)…(1﹣ )(1﹣
)(1﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】“C919”大型客机首飞成功,激发了同学们对航空科技的兴趣,如图是某校航模兴趣小组获得的一张数据不完整的航模飞机机翼图纸,图中AB∥CD,AM∥BN∥ED,AE⊥DE,请根据图中数据,求出线段BE和CD的长.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,结果保留小数点后一位)
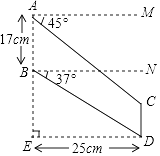
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连接DE和DB,过点E作EF⊥AB,垂足为F,交BD于点P.
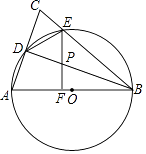
(1)求证:AD=DE;
(2)若CE=2,求线段CD的长;
(3)在(2)的条件下,求△DPE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读材料)
我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决一些图形问题.
在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为
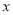 的正方形,乙种纸片是边长为
的正方形,乙种纸片是边长为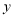 的正方形,丙种纸片是长为
的正方形,丙种纸片是长为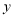 ,宽为
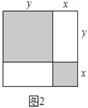
,宽为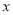 的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
的长方形,并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.(理解应用)
(1)观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(拓展升华)
(2)利用(1)中的等式解决下列问题.
①已知
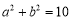 ,
,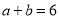 ,求
,求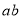 的值;
的值;②已知
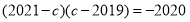 ,求
,求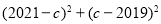 的值.
的值.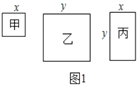
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
相关试题

