搜索
【题目】下列对一元二次方程x2+x﹣3=0根的情况的判断，正确的是（ ）
A. 有两个不相等实数根 B. 有两个相等实数根
C. 有且只有一个实数根 D. 没有实数根
参考答案：
【答案】A
【解析】
根据方程的系数结合根的判别式，即可得出△=13＞0，进而即可得出方程x2+x﹣3=0有两个不相等的实数根．
∵a=1，b=1，c=﹣3，
∴△=b2﹣4ac=12﹣4×（1）×（﹣3）=13＞0，
∴方程x2+x﹣3=0有两个不相等的实数根，
故选A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校举办“我的中国梦”演讲比赛，有9名学生参加比赛，他们比赛的最终成绩各不相同，取前5名同学参加决赛．其中一名同学知道自己的分数后，要判断自己能否进入决赛，只需要知道这9名同学分数的( )
A. 中位数B. 众数C. 平均数D. 方差
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，点C在AB的延长线上，AD平分∠CAE交⊙O于点D，且AE⊥CD，垂足为点E．
（1）求证：直线CE是⊙O的切线．
（2）若BC=3，CD=3
，求弦AD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，AB是⊙O的直径，OD⊥弦BC于点F，且交⊙O于点E，若∠AEC=∠ODB．
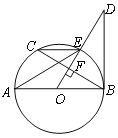
（1）判断直线BD和⊙O的位置关系，并给出证明；
（2）当AB=10，BC=8时，求BD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D．过点C作CF∥AB，在CF上取一点E，使DE=CD，连接AE．对于下列结论：①AD=DC；②△CBA∽△CDE；③
；④AE为⊙O的切线，一定正确的结论全部包含其中的选项是（ ）
A．①② B．①②③ C．①④ D．①②④
-
科目： 来源： 题型：
查看答案和解析>>【题目】方程x2﹣2x=3可以化简为（ ）
A. （x﹣3）（x+1）=0 B. （x+3）（x﹣1）=0 C. （x﹣1）2=2 D. （x﹣1）2+4=0
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于x的方程：(1－m)x| m |＋2＝0是一元一次方程．求m的值和方程的解．
相关试题
