【题目】已知:在纸面上有一数轴,如图所示,点O为原点,点A1、A2、A3、…分别表示有理数1、2、3、…,点B1、B2、B3、…分别表示有理数﹣1、﹣2、﹣3、….
![]()
(1)折叠纸面:
①若点A1与点B1重合,则点B2与点 重合;
②若点B1与点A2重合,则点A5与有理数 对应的点重合;
③若点B1与A3重合,当数轴上的M、N(M在N的左侧)两点之间的距离为9,且M、N两点经折叠后重合时,则M、N两点表示的有理数分别是 , ;
(2)拓展思考:
点A在数轴上表示的有理数为a,用|a|表示点A到原点O的距离.
①|a﹣1|是表示点A到点 的距离;
②若|a﹣1|=3,则有理数a= ;
③若|a﹣1|+|a+2|=5,则有理数a= .
参考答案:
【答案】(1) ①A2,②B4, ③﹣3.5,5.5;(2) ①A1,②﹣2或4,③﹣3或2
【解析】
(1)①根据中心对称,可得对称中心,根据对称中心,可得点的对应点;
②根据中心对称,可得对称中心,根据对称中心,可得点的对应点;
③根据中心对称,可得对称中心,根据对称中心到任意一点的距离相等,可得点的对应点;
(2)①根据两点间的距离公示,可得答案;
②根据数轴上到一点距离相等点有两个,位于该点的左右,可得答案;
③根据解含绝对值符号的一元一次方程,可得方程的解.
解:(1)折叠纸面:
①若点A1与点B1重合,则点B2与点 A2重合;
②若点B1与点A2重合,则点A5与有理数 B4对应的点重合;
③若点B1与A3重合,当数轴上的M、N(M在N的左侧)两点之间的距离为9,且M、N两点经折叠后重合时,则M、N两点表示的有理数分别是﹣3.5,5.5;
(2)拓展思考:
点A在数轴上表示的有理数为a,用|a|表示点A到原点O的距离.
①|a﹣1|是表示点A到点 A1的距离;
②若|a﹣1|=3,则有理数a=﹣2或4;
③若|a﹣1|+|a+2|=5,则有理数a=﹣3或 2,
故答案为:A2,B4﹣3.5,5.5,A1,﹣2或4,﹣3或2.
-
科目: 来源: 题型:
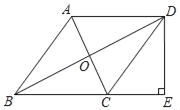
查看答案和解析>>【题目】如图,O为△ABC边AC的中点,AD∥BC交BO的延长线于点D,连接DC,DB平分∠ADC,作DE⊥BC,垂足为E.
(1)求证:四边形ABCD为菱形;
(2)若BD=8,AC=6,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏在研究数学问题时遇到一个定义:将三个已经排好顺序数:x1,x2,x3,称为数列x1,x2,x3.计算|x1|,
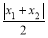 ,
,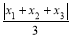 ,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,
,将这三个数的最小值称为数列x1,x2,x3的最佳值.例如,对于数列2,-1,3,因为|2|=2,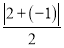 =
=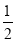 ,
,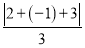 =
=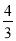 ,所以数列2,-1,3的最佳值为
,所以数列2,-1,3的最佳值为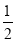 .
.小敏进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的最佳值.如数列-1,2,3的最佳值为
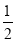 ;数列3,-1,2的最佳值为1;….经过研究,小敏发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为
;数列3,-1,2的最佳值为1;….经过研究,小敏发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,最佳值的最小值为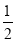 .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:(1)数列-4,-3,1的最佳值为______;
(2)将“-4,-3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的最佳值的最小值为______,取得最佳值最小值的数列为______(写出一个即可);
(3)将2,-9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的最佳值为1,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的边长为4,对角线相交于点P,顶点A、C分别在x轴、y轴的正半轴上,抛物线L经过0、P、A三点,点E是正方形内的抛物线上的动点.
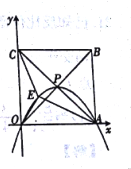
(1)点P的坐标为______
(2)求抛物线L的解析式.
(3)求△OAE与△OCE的面积之和的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有个填写运算符号的游戏:在“
 ”中的每个□内,填入
”中的每个□内,填入 中的某一个(可重复使用),然后计算结果.
中的某一个(可重复使用),然后计算结果.(1)计算:
 ;
;(2)若请推算
 □内的符号;
□内的符号;(3)在“
 ”的□内填入符号后,使计算所得数最小,直接写出这个最小数.
”的□内填入符号后,使计算所得数最小,直接写出这个最小数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处. 已知折痕AE=
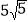 cm,且tan∠EFC=
cm,且tan∠EFC=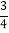 ,则矩形ABCD的周长为______cm.
,则矩形ABCD的周长为______cm.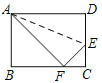
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线),继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得7条折痕,那么对折四次可以得到 条折痕,如果对折
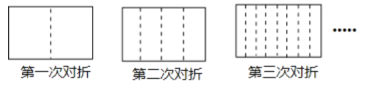 次,可以得到 条折痕.
次,可以得到 条折痕.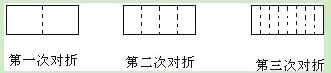
相关试题

