【题目】如图,△ABC中,∠C=90°,AB=10 cm,BC=6 cm,动点P从点C出发,以每秒2 cm的速度按C→A的路径运动,设运动时间为t秒.
(1)出发2秒时,△ABP的面积为 cm2;
(2)当t为何值时,BP恰好平分∠ABC?

参考答案:
【答案】(1)12;(2) ![]() .
.
【解析】试题分析:(1)利用勾股定理得出AC=8cm,进而表示出AP的长,进而得出答案;
(2)过点P作PD⊥AB于点D,由HL证明Rt△BPD≌Rt△BPC,得出BD=BC=6cm,因此AD=10-6=4cm,设PC=tcm,则PA=(8-t)cm,由勾股定理得出方程,解方程即可.
试题解析:(1)∵∠C=90°,AB=10cm,BC=6cm,
∴AC=8cm,
根据题意可得:PC=4cm,则AP=4cm,
故△ABP的面积为: ![]() ×AP×BC=
×AP×BC=![]() ×4×6=12(cm2);
×4×6=12(cm2);
(2)解:过点P作PG⊥AB于G,则∠BGP=90°.

∵∠C=90°,
∴∠BGP=∠C.
∵BP平分∠ABC,
∴∠CBP=∠ABP.
又∵BP=BP,
∴△BCP≌△BGP.
∴BG=BC=6,PG=PC=2t.
∴PA=8-2t,AG=10-6=4.
在Rt△APG中, AG2+PG2=AP2.
∴42+(2t)2=(8-2t)2
解得t=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=21,BC=13,D是AC边上一点,BD=12,AD=16,E是边AB的中点,求线段DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列因式分解正确的是( )
A. x2﹣4=(x+4)(x﹣4) B. x2﹣2x﹣15=(x+3)(x﹣5)
C. 3mx﹣6my=3m(x﹣6y) D. 2x+4=2(x+4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(b﹣c)2=4(1﹣b)(c﹣1),则b+c的值是( )
A.﹣1B.0C.1D.2
-
科目: 来源: 题型:
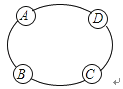
查看答案和解析>>【题目】如图是某汽车维修公司的维修点在环形公路上的分布图.公司在年初分配给A,B,C,D四个维修点某种配件各50件.在使用前发现需将A,B,C,D四个维修点的这批配件分别调整为40,45,54,61件,但调整只能在相邻维修点之间进行,那么要完成上述调整,最少的调动件次为多少?说明理由.(注:n件配件从一个维修点调整到相邻维修点的调动件次为n)
-
科目: 来源: 题型:
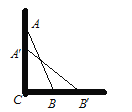
查看答案和解析>>【题目】一架长2.5米的梯子AB如图所示斜靠在一面墙上,这时梯足B离墙底C(∠C=90°)的距离BC为0.7米.
(1)求此时梯顶A距地面的高度AC;
(2)如果梯顶A下滑0.9米,那么梯足B在水平方向,向右滑动了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.在同一平面内,过直线外一点,有无数条直线与已知直线垂直
B.由平移得到的两个图形的各组对应点连线互相垂直
C.命题“一个角的余角一定是锐角”是真命题
D.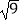 是无理数
是无理数
相关试题

