【题目】如图1,在四边形ABCD中,AB∥CD,∠ABC=90°,动点P从A点出发,沿A→D→C→B匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
⑴①AD= , CD= , BC= ; (填空)
②当点P运动的路程x=8时,△ABP的面积为y= ; (填空)
⑵求四边形ABCD的面积
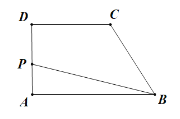
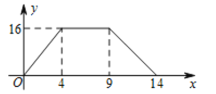
图1 图2
参考答案:
【答案】(1)①4,5,5;②16;(2)面积为26.
【解析】
(1)①根据图2的图像,当点P运动到点D时,运动距离是4,即可知道AD的长度,进而知道CD、BC的长度;②点P运动的路程是8时,点P在CD上,即可得到△ABP的面积;
(2)根据(1)所得的结论,可以求得AB的长度,进而计算四边形ABCD的面积.
(1)①根据函数图像可知:AD=4,CD=5,BC=5;
故答案为:4,5,5.
②当点P运动到CD上时,△ABP的面积达到最大值,
∴x=8时,△ABP的面积为16;
故答案为:16.
(2)当点P运动到点D时,有△ABP的面积为16,
∴![]() ,
,
∴AB=8
∴四边形ABCD的面积为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=AD,AC=AE,BC=DE,点E在BC上.

(1)求证:△ABC≌△ADE;(2)求证:∠EAC=∠DEB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D.DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=
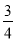 ,求OE的长.
,求OE的长.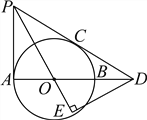
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习“利用三角函数测高”后,某综合实践活动小组实地测量了凤凰山与中心广场的相对高度AB,其测量步骤如下:
(1)在中心广场测点C处安置测倾器,测得此时山顶A的仰角∠AFH=30°;
(2)在测点C与山脚B之间的D处安置测倾器(C、D与B在同一直线上,且C、D之间的距离可以直接测得),测得此时山顶上红军亭顶部E的仰角∠EGH=45°;
(3)测得测倾器的高度CF=DG=1.5米,并测得CD之间的距离为288米;
已知红军亭高度为12米,请根据测量数据求出凤凰山与中心广场的相对高度AB.(
 取1.732,结果保留整数)
取1.732,结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABO中,斜边AB=1.若OC∥BA,∠AOC=36°,则( )
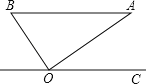
A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点A到OC的距离为cos36°sin54°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,∠A=40°.点P是射线AB上一动点(与点A不重合),CE、CF分别平分∠ACP和∠DCP交射线AB于点E、F.
(1)求∠ECF的度数;
(2)随着点P的运动,∠APC与∠AFC之间的数量关系是否改变?若不改变,请求出此数量关系;若改变,请说明理由;
(3)当∠AEC=∠ACF时,求∠APC的度数.

-
科目: 来源: 题型:
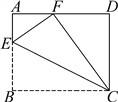
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为___.
相关试题

