【题目】某同学在求多边形的内角和时,多算了一个内角的度数,求得内角和为1 560°,问这个内角是多少度?这个多边形的边数是多少?
参考答案:
【答案】这个内角是120°,这个多边形的边数是10.
【解析】试题分析:设这个多边形的边数为n,多算的这个内角为α,根据多边形的内角和公式可得(n-2)·180°+α=1 560°,然后根据多边形每个内角的取值范围0°<α<180°列不等式,即可求出多边形的边数,进而求出这个内角的度数.
解:设这个多边形的边数为n,多算的这个内角为α,则有:
(n-2)·180°+α=1 560°.
∴α=1 560°-(n-2)·180°.
显然:0°<α<180°,
∴0°<1 560°-(n-2)·180°<180°.解得9![]() <n<10
<n<10![]() .
.
∴n=10.
∴α=1 560°-(10-2)·180°=120°.
答:这个内角是120°,这个多边形的边数是10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=2x2﹣2
 x+1与坐标轴的交点个数是( )
x+1与坐标轴的交点个数是( )
A.0
B.1
C.2
D.3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于C、D.
(1)求∠CBD的度数;
(2)当点P运动时,那么∠APB:∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把一条抛物线先向上平移3个单位长度,然后绕原点选择180°得到抛物线y=x2+5x+6,则原抛物线的解析式是( )
A.y=﹣(x﹣ )2﹣
)2﹣ 
B.y=﹣(x+ )2﹣
)2﹣ 
C.y=﹣(x﹣ )2﹣
)2﹣ 
D.y=﹣(x+ )2+
)2+ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )

A. ∠BCA=∠F B. BC∥EF C. ∠A=∠EDF D. AD=CF
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=
 BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=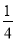 BC 成立的个数有( )
BC 成立的个数有( )
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC,∠A、∠B、∠C之和为多少?为什么?
解:∠A+∠B+∠C=180°
理由:作∠ACD=∠A,并延长BC到E
∵∠ACD=∠ (已作)
AB∥CD( )
∴∠B= ( )
而∠ACB+∠ACD+∠DCE=180°
∴∠ACB+ + =180°( )

相关试题

