【题目】如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2![]() ;
;
④四边形ACEB的面积是16.
则以上结论正确的是( )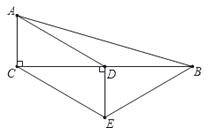
A.①②③
B.①②④
C.①③④
D.②④
参考答案:
【答案】A
【解析】解:①∵∠ACB=90°,DE⊥BC,
∴∠ACD=∠CDE=90°,
∴AC∥DE,
∵CE∥AD,
∴四边形ACED是平行四边形,故①正确;
②∵D是BC的中点,DE⊥BC,
∴EC=EB,
∴△BCE是等腰三角形,故②正确;
③∵AC=2,∠ADC=30°,
∴AD=4,CD=2![]() ,
,
∵四边形ACED是平行四边形,
∴CE=AD=4,
∵CE=EB,
∴EB=4,DB=2![]() ,
,
∴CB=4![]() ,
,
∴AB=![]() =2
=2![]() ,
,
∴四边形ACEB的周长是10+2![]() 故③正确;
故③正确;
④四边形ACEB的面积:![]() ×2×4
×2×4![]() +
+![]() ×4
×4![]() ×2=8
×2=8![]() , 故④错误,
, 故④错误,
故选:A.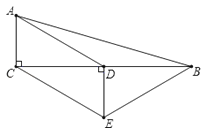
证明AC∥DE,再由条件CE∥AD可证明四边形ACED是平行四边形;根据线段的垂直平分线证明AE=EB可得△BCE是等腰三角形;首先利用三角函数计算出AD=4,CD=2![]() , 再算出AB长可得四边形ACEB的周长是10+2
, 再算出AB长可得四边形ACEB的周长是10+2![]() , 利用△ACB和△CBE的面积和可得四边形ACEB的面积.
, 利用△ACB和△CBE的面积和可得四边形ACEB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D。
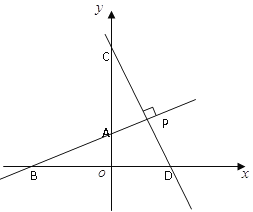
(1)求出点A、点B的坐标。
(2)请求出直线CD的解析式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】用如图所示的长31.4cm,宽5cm的长方形,围成一个圆柱体,求需加上的两个底面圆的面积是多少平方厘米?
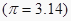

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点A′处,点B落在点B′处,若∠2=40°,则图中∠1的度数为( )

A. 115° B. 120° C. 130° D. 140°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有理数的倒数是它本身,这个数是( )
A.0
B.1
C.﹣1
D.1或﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各题运算正确的是( )
A.3x+3y=6xy
B.x+x=x2
C.﹣9y2+16y2=7
D.9a2b﹣9a2b=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个棱柱有12条棱,那么它的底面一定是( )
A.十八边形
B.六边形
C.四边形
D.八边形
相关试题

