【题目】如图,D为ABC的AB边上一点,E为AC延长线上的一点,且CE=BD。
(1)当AB=AC时,求证:DE>BC
(2)当AB≠AC时,DE与BC有何大小关系?给出结论,画出图形,并证明。

参考答案:
【答案】(1)见解析;(2)见解析
【解析】试题分析:
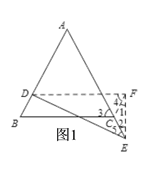
(1)如图1,过点D作DF∥BC,过点C作CF∥AB,连接EF,从而可得DF=BC,这样就把分散的线段集中到了△DEF中,只需证DE>DF即可;易证∠1=∠2,∠3=∠4,∠3>∠5,从而可得∠DFE>∠DEF,∴DE>DF,从而得到:DE>BC;
(2)当AB![]() AC时,我们要分AB>AC和AB<AC两种情况来讨论,
AC时,我们要分AB>AC和AB<AC两种情况来讨论,
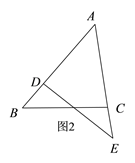
其中:①当AB>AC,且AB=AE时,如图2,结合已知条件此时我们易证△ABC≌△AED,从而得到BC=DE;
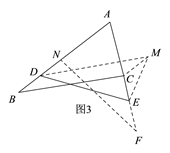
②当AB>AC,且AB>AE时,如图3,延长AE到F,使AF=AB,在AB上截取AN=AC,易证△ABC≌△AFN,得到∠F=∠B;再过D作DM∥BC,过C作CM∥BD,得到四边形DBCM是平行四边形,由此可得∠DMC=∠B=∠F,DM=BC;连接ME,则法通过在△DME中证∠DEM>∠DME得到DM>DE,从而得到BC>DE;
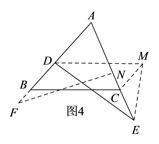
③当AB>AC,且AB<AE时,如图4,延长AB到F,使AF=AE,在AE上截取AN=AD,连接NF,易证△AFN≌△AED,可得∠F=∠AED,由∠ABC>∠F得到∠ABC>∠AED;再作DM∥BC,CM∥AB,可得四边形DBCM是平行四边形,得到DM=BC,∠DMC=∠ABC,就可得∠DMC>∠AED;连接ME,在△DME中通过证∠DME>∠DEM,得到DE>DM,就可得到DE>BC;
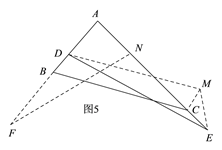
④当AB<AC<AE时,如图5,延长AB至F,使AF=AE,在AC上截取AN=AD;过点D作DM∥BC,过点C作CM∥AB,连接ME;同上可证:DE>BC.
试题解析:
(1)作DF∥BC,CF∥BD(如图1),
得□BCFD,从而∠DFC=∠B,
DF=BC,CF=BD.
又BD=CE,∴CF=CE,
∴∠1=∠2.
∵AB=AC,∴∠ACB=∠B.
而∠DFE=∠DFC+∠1=∠B+∠1
=∠ACB+∠2>∠AED+∠2=∠DEF,
即在△DEF中,∵∠DFE>∠DEF,
∴DE>DF,即DE>BC.
(2)当AB≠AC时,DE与BC的大小关系如下:
当AB>AC但AB=AE时,DE=BC;
当AB>AC且AB>AE时,DE<BC;
当AB>AC但AB<AE时,DE>BC;
当AB<AC时,DE>BC.
证明如下:
①当AB>AC但AB=AE时(如图2),
∵BD=CE,∴AB-BD=AE-CE,即AD=AC.
在△ABC和△AED中,
∵AB=AE,∠A=∠A,AC=AD,
∴△ABC≌△AED(SAS),∴BC=ED;
②当AB>AC且AB>AE时,
延长AE到F,使AF=AB,
在AB上截取AN=AC(如图3),连结NF.
在△ABC和△AFN中,
∵AB=AF,∠A=∠A,AC=AN,
∴△ABC≌△AFN(SAS),∴∠B=∠F.
∵∠AED>∠F,∴∠AED>∠B.
过D点作DM∥BC,过点C作CM∥AB,连结EM,
则四边形DBCM为平行四边形,∴∠DMC=∠B,CM=BD,DM=BC,
∵BD=CE,∴CM=CE,∴∠CME=∠CEM,
∵∠DMC=∠B<∠AED,∴∠CME+∠DMC<∠AED+∠CEM,
即∠DME<∠DEM,∴DE<DM,∴DE<BC;
③当AB>AC但AB<AE时,延长AB到F,使AF=AE,
在AE上截取AN=AD(如图4),连结NF,
在△AFN和△AED中,
∵AF=AE,∠A=∠A,AN=AD,
∴△AFN≌△AED(SAS),
∴∠F=∠AED,
∵∠ABC>∠F,
∴∠ABC>∠AED,
过D点作DM∥BC,过点C作CM∥AB,连接EM,
则四边形DBCM为平行四边形,
∴∠DMC=∠ABC,CM=BD,
∵BD=CE,
∴CM=CE,
∴∠CME=∠CEM,
∵∠DMC=∠ABC>∠AED,
∴∠DMC+∠CME>∠AED+∠CEM,
即∠DME>∠DEM,
∴ DE>DM,
∴ DE>BC;
④当AB<AC时,此时,AB必小于AE,即AB<AE
延长AB到F,使AF=AE,在AE上截取AN=AD(如图5).
连结NF.在△AFN和△AED中,
∵AF=AE,∠A=∠,AN=AD,∴△AFN≌△AED(SAS),
∴∠F=∠AED,即∠F=∠4.∵∠ABC>∠F,∴∠ABC>∠AED,
过D作DM∥BC,过点C作CM∥AB,连结CM,
则四边形DBCM平行四边形,∴∠DMC=∠ABC,CM=BD,DM=BC,
∵BD=CE,∴CM=CE,∴∠CME=∠CEM.∵∠DMC=∠ABC>∠AED,
∴∠DMC+∠CDE>∠AED+∠CEM,即∠DME>∠DEM,
∴DE>DM,
∴DE>BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据35,38,37,36,37,36,37,35的众数是( )
A.35
B.36
C.37
D.38 -
科目: 来源: 题型:
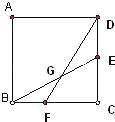
查看答案和解析>>【题目】已知正方形ABCD的边长为4cm,E,F分别为边DC,BC上的点,BF=1cm,CE=2cm,BE,DF相交于点G,求四边形CEGF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一间摄影展览厅,其东、西面各有一个入口A、B,南面为出口C,北面分别有两个出口D、E,摄影爱好者郑浩任选一个入口进入展览厅,参观结束后,任选一个出口离开。
(1)郑浩从进入到离开共有多少种可能的结果?请画出树形图;
(2)求出郑浩从入口A进入展览厅并从北面出口离开的概率。

-
科目: 来源: 题型:
查看答案和解析>>【题目】一队卡车运一批货物,若每辆卡车装7吨货物,则剩余10吨货物装不完;若每辆卡车装8吨货物,则最后一辆卡车只装3吨货物就装完了这批货物,那么这批货物共有吨.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,C是⊙O上的一点,连结AC并延长至D,使CD=AC,连结BD,作CE⊥BD,垂足为E。
(1)线段AB与DB的大小关系为 ,请证明你的结论;
(2)判断CE与⊥⊙O的位置关系,并证明;
(3)当△CED与四边形ACEB的面积比是1:7时,试判断△ABD的形状,并证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】人体中小淋巴细胞的直径若为0.0000000045m,用科学记数法表示小淋巴细胞的直径为_____m.
相关试题

