Question

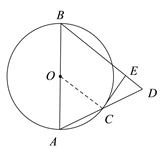
【题目】如图，已知AB是⊙O的直径，C是⊙O上的一点，连结AC并延长至D，使CD=AC，连结BD，作CE⊥BD，垂足为E。

（1）线段AB与DB的大小关系为 ，请证明你的结论；

（2）判断CE与⊥⊙O的位置关系，并证明；

（3）当△CED与四边形ACEB的面积比是1:7时，试判断△ABD的形状，并证明。

Answer 1

【答案】(1)AB=DB,理由见解析；（2）CE是⊙Ｏ的切线，理由见解析；（3）△ABD为等边三角形，理由见解析

【解析】试题分析：

（1）如图，连接BC，由AB是⊙O的直径可得：BC⊥AD，再由AC=CD，可得BC是AD的垂直平分线，从而由线段垂直平分线的性质可得AB=BD；

（2）如图，连接OC，由已知：OA=OB，AC=CD，可得OC是△ABD的中位线，从而得到OC∥BD，又∵CE⊥BD，可得CE⊥OC，就可得到CE是⊙O的切线；

（3）如图，由已知S△CDE:S四边形ACEB=1：7易得S△CDE:S△ABD=1：8，连接BC，由AC=CD=AD可得S△ABD=2S△BCD，∴S△CDE:2S△BCD=1：8，则S△CDE:S△BCD=1：4；由（1）和已知易证△BCD∽△CED，从而可得： ，∴即BD=2CD，再由AB=BD，AD=2BD，就可得到：AB=BD=AD，∴△ABD是等边三角形.

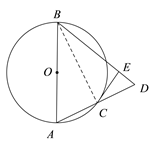
试题解析：

（１）线段AB=DB，

证明如下：

连结BC，∵AB是⊙Ｏ的直径，

∴∠ACB＝90°，即BC⊥AD．

又∵AC＝CD，∴BC垂直平分线段AD，

∴AB＝DB；

（２）CE是⊙Ｏ的切线．

证明如下：

连结OC．

∵点O为AB的中点，点C为AD的中点，

∴OC为△ABD的中位线，∴OC∥BD，

又∵CE⊥BD，∴CE⊥OC，∴CE是⊙O的切线；

（３）△ABD为等边三角形．

证明如下：

由＝，

得＝，

∴＝，

即＝，∴＝， ＝，

∵∠D＝∠D，∠CED＝∠BCD＝90°，∴△CED∽△BCD，

∴＝，即＝，∴＝，

在Rt△BCD中，∵CD＝BD，

∴∠CBD＝30°，∴∠D＝60°，又∵AB＝DB，

∴△ABD为等边三角形．