搜索
【题目】如图1所示，从边长为a的正方形纸片中减去一个边长为b的小正方形，再沿着线段AB剪开，把剪成的两张纸拼成如图2的等腰梯形（其面积= 
）.
（1）设图1中阴影部分面积为S1，图2中阴影部分面积为S2，请直接用含a、b的式子表示S1和S2；
（2）请写出上述过程所揭示的乘法公式．
参考答案：
【答案】（1）
， 
；（2）
.
【解析】试题分析：（1）先用大正方形的面积减去小正方形的面积，即可求出S1，再根据梯形的面积公式即可求出S2；
（2）根据（1）得出的值，直接可写出乘法公式（a+b）（a-b）=a2-b2．
试题解析：（1）∵大正方形的边长为a，小正方形的边长为b，
∴S1=a2﹣b2，
S2=
（2a+2b）（a﹣b）=（a+b）（a﹣b）；
（2）根据题意得：
（a+b）（a﹣b）=a2﹣b2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，大楼AN上悬挂一条幅AB，小颖在坡面D处测得条幅顶部A的仰角为30°，沿坡面向下走到坡脚E处，然后向大楼方向继续行走10米来到C处，测得条幅的底部B的仰角为45°，此时小颖距大楼底端N处20米．已知坡面DE=20米，山坡的坡度i=1：
（即tan∠DEM=1： ），且D，M，E，C，N，B，A在同一平面内，E，C，N在同一条直线上，求条幅的长度（结果精确到1米）（参考数据： ≈1.73，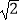 
≈1.41）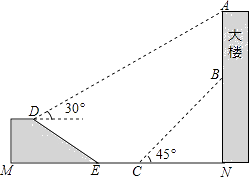
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示的直角坐标系中，△ABC的顶点坐标分别是A(－4，－1)，B(1，1)，C(－1，4)；点
是△ABC内一点，当点平移到点
时．①请写出平移后新
三个顶点的坐标；②求
的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别为(－1，0)，(3，0)，现同时将点A，B分别向上平移2个单位长度，再向右平移1个单位长度，得到A，B的对应点C，D，连接AC，BD，CD.
(1)直接写出点C，D的坐标，求出四边形ABDC的面积；
(2)在x轴上是否存在一点F，使得三角形DFC的面积是三角形DFB面积的2倍，若存在，请求出点F的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°．
（1）求证：四边形ABCD是矩形．
（2）若∠ADF：∠FDC=3：2，DF⊥AC，则∠BDF的度数是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】问题背景：在△ABC中，AB、BC、AC三边的长分别为
、
、
，求此三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．（1）请你将△ABC的面积直接填写在横线上： ．
思维拓展：
（2）我们把上述求△ABC面积的方法叫做构图法．如果△ABC三边的长分别
a、
a、
a（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，并求出它的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知E，F分别是AB、CD上的动点，P也为一动点．
（1）如图1，若AB∥CD，求证：∠P＝∠BEP＋∠PFD；
（2）如图2，若∠P＝∠PFD－∠BEP，求证：AB∥CD；
（3）如图3，AB∥CD，移动E，F使得∠EPF＝90°，作∠PEG＝∠BEP，求
的值．
相关试题
