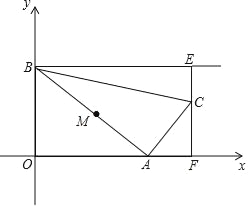
【题目】如图,点A是x轴非负半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.
(Ⅰ)当t=2时,求点M的坐标;
(Ⅱ)设ABCE的面积为S,当点C在线段EF上时,求S与t之间的函数关系式,并写出自变量t的取值范围;
(Ⅲ)当t为何值时,BC+CA取得最小值.
参考答案:
【答案】(1)(1,2);(2)S=![]() t+8(0≤t≤8);(3)当t=0时,BC+AC有最小值
t+8(0≤t≤8);(3)当t=0时,BC+AC有最小值
【解析】试题分析:(I)过M作MG⊥OF于G,分别求OG和MG的长即可;
(II)如图1,同理可求得AG和OG的长,证明△AMG≌△CAF,得:AG=CF=![]() t,AF=MG=2,分别表示EC和BE的长,代入面积公式可求得S与t的关系式;并求其t的取值范围;
t,AF=MG=2,分别表示EC和BE的长,代入面积公式可求得S与t的关系式;并求其t的取值范围;
(III)证明△ABO∽△CAF,根据勾股定理表示AC和BC的长,计算其和,根据二次根式的意义得出当t=0时,值最小.
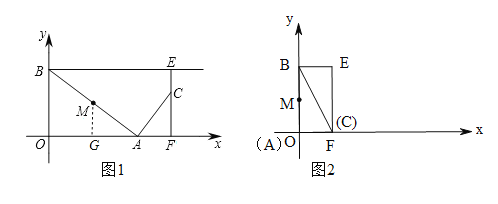
试题解析:解:(I)如图1,过M作MG⊥OF于G,∴MG∥OB,当t=2时,OA=2.∵M是AB的中点,∴G是AO的中点,∴OG=![]() OA=1,MG是△AOB的中位线,∴MG=
OA=1,MG是△AOB的中位线,∴MG=![]() OB=
OB=![]() ×4=2,∴M(1,2);
×4=2,∴M(1,2);
(II)如图1,同理得:OG=AG=![]() t.∵∠BAC=90°,∴∠BAO+∠CAF=90°.∵∠CAF+∠ACF=90°,∴∠BAO=∠ACF.∵∠MGA=∠AFC=90°,MA=AC,∴△AMG≌△CAF,∴AG=CF=
t.∵∠BAC=90°,∴∠BAO+∠CAF=90°.∵∠CAF+∠ACF=90°,∴∠BAO=∠ACF.∵∠MGA=∠AFC=90°,MA=AC,∴△AMG≌△CAF,∴AG=CF=![]() t,AF=MG=2,∴EC=4﹣
t,AF=MG=2,∴EC=4﹣![]() t,BE=OF=t+2,∴S△BCE=
t,BE=OF=t+2,∴S△BCE=![]() ECBE=
ECBE=![]() (4﹣
(4﹣![]() t)(t+2)=﹣
t)(t+2)=﹣![]() t2+
t2+![]() t+4;
t+4;
S△ABC=![]() ABAC=
ABAC=![]()
![]()
![]() =
=![]() t2+4,∴S=S△BEC+S△ABC=
t2+4,∴S=S△BEC+S△ABC=![]() t+8.
t+8.
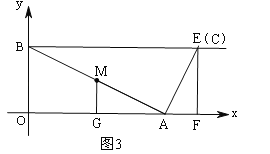
当A与O重合,C与F重合,如图2,此时t=0,当C与E重合时,如图3,AG=EF,即 ![]() t=4,t=8,∴S与t之间的函数关系式为:S=
t=4,t=8,∴S与t之间的函数关系式为:S=![]() t+8(0≤t≤8);
t+8(0≤t≤8);
(III)如图1,易得△ABO∽△CAF,∴![]() =
=![]() =
=![]() =2,∴AF=2,CF=
=2,∴AF=2,CF=![]() t,由勾股定理得:AC=
t,由勾股定理得:AC=![]() =
=![]() =
=![]() ,BC=
,BC=![]() =
=![]() =
=![]() ,∴BC+AC=(
,∴BC+AC=( ![]() +1)
+1)![]() ,∴当t=0时,BC+AC有最小值.
,∴当t=0时,BC+AC有最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
 的图像与反比例函数
的图像与反比例函数 的图像交于第一、三象限内的
的图像交于第一、三象限内的 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 在
在 轴负半轴上,
轴负半轴上, ,且四边形
,且四边形 是平行四边形,点
是平行四边形,点 的纵坐标为
的纵坐标为 .
.(1)求该反比例函数和一次函数的表达式;
(2)连接
 ,求
,求 的面积;
的面积;(3)直接写出关于
 的不等式
的不等式 的解集.
的解集.
-
科目: 来源: 题型:
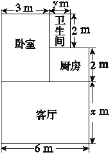
查看答案和解析>>【题目】丁丁家买了一套安置房,地面结构如图所示.
(1)写出用含x、y的式子表示地面的总面积;
(2)如果x=4 m,y=1.5 m,铺1 m2地砖的平均费用为80元,求铺地砖的总费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正六边形ABCDEF的中心与坐标原点O重合,AF∥x轴,将正六边形ABCDEF绕原点O顺时针旋转n次,每次旋转60°,当n=2018时,顶点A的坐标为_____.
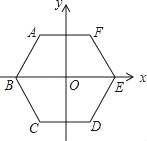
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD(AB<AD).
(1)请用直尺和圆规按下列步骤作图,保留作图痕迹;
①以点A为圆心,以AD的长为半径画弧交边BC于点E,连接AE;
②作∠DAE的平分线交CD于点F;
③连接EF;
(2)在(1)作出的图形中,若AB=8,AD=10,则tan∠FEC的值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=mx2﹣(m+n)x+n(m<0)的图象与y轴正半轴交于A点.
(1)求证:该二次函数的图象与x轴必有两个交点;
(2)设该二次函数的图象与x轴的两个交点中右侧的交点为点B,若∠ABO=45°,将直线AB向下平移2个单位得到直线l,求直线l的解析式;
(3)在(2)的条件下,设M(p,q)为二次函数图象上的一个动点,当﹣3<p<0时,点M关于x轴的对称点都在直线l的下方,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,AF⊥CD于点F,若AE=4,AF=6,且ABCD的周长为40,则ABCD的面积为( )
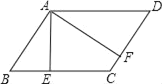
A. 24B. 36C. 40D. 48
相关试题

