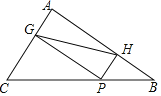
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
参考答案:
【答案】(1)证明见解析;(2)见解析.
【解析】
(1)根据“矩形的定义”证明结论;
(2)连结AP.当AP⊥BC时AP最短,结合矩形的两对角线相等和面积法来求GH的值.
(1)证明∵AC=9AB=12BC=15,
∴AC2=81,AB2=144,BC2=225,
∴AC2+AB2=BC2,
∴∠A=90°.
∵PG⊥AC,PH⊥AB,
∴∠AGP=∠AHP=90°,
∴四边形AGPH是矩形;
(2)存在.理由如下:
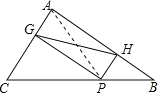
连结AP.
∵四边形AGPH是矩形,
∴GH=AP.
∵当AP⊥BC时AP最短.
∴9×12=15AP.
∴AP=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有
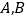 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台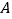 型和5台
型和5台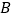 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台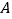 型和7台
型和7台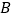 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台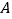 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台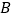 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.(1)分别求每台
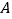 型,
型, 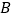 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?(2)若不同数量的
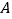 型和
型和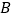 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】我市在旧城改造中,计划在市内一块如下图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价
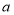 元,则购买这种草皮至少需要______元.
元,则购买这种草皮至少需要______元.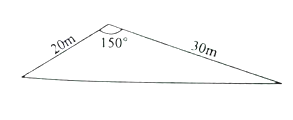
-
科目: 来源: 题型:
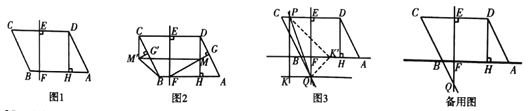
查看答案和解析>>【题目】如图1,在
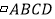 中,
中,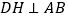 于点
于点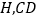 的垂直平分线交
的垂直平分线交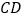 于点
于点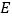 ,交
,交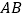 于点
于点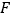 ,
,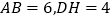 ,
,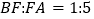 .
.
(1)如图2,作
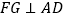 于点
于点 ,交
,交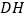 于点
于点 ,将
,将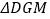 沿
沿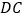 方向平移,得到
方向平移,得到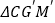 ,连接
,连接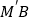 .
.①求四边形
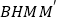 的面积;
的面积;②直线
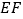 上有一动点
上有一动点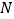 ,求
,求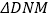 周长的最小值.
周长的最小值.(2)如图3.延长
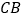 交
交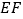 于点
于点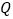 .过点
.过点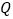 作
作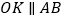 ,过
,过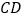 边上的动点
边上的动点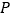 作
作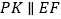 ,并与
,并与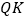 交于点
交于点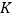 ,将
,将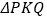 沿直线
沿直线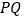 翻折,使点
翻折,使点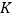 的对应点
的对应点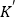 恰好落在直线
恰好落在直线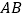 上,求线段
上,求线段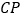 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分
人数/人
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
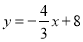 与
与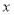 轴、
轴、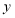 轴分别相交于点
轴分别相交于点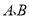 ,设
,设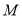 是线段
是线段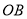 上一点,若将△
上一点,若将△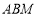 沿
沿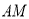 折叠,使点
折叠,使点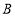 恰好落在
恰好落在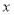 轴上的点
轴上的点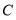 处。求:
处。求: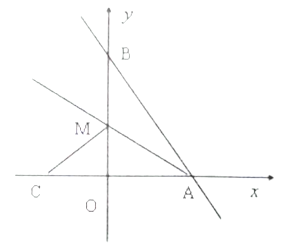
(1)点
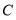 的坐标;
的坐标;(2)直线
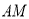 所对应的函数关系式.
所对应的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点
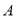 和点
和点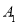 是线段
是线段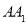 的两个端点,线段
的两个端点,线段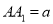 ,点
,点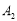 是点
是点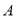 和点
和点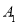 的对称中心,点
的对称中心,点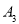 是点
是点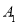 和点
和点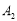 的对称中心,以此类推,(图中未画出)点
的对称中心,以此类推,(图中未画出)点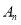 是点
是点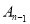 和点
和点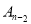 的对称中心.(
的对称中心.(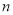 为正整数)
为正整数)
(1)填空:线段
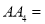 ____________ ;线段
____________ ;线段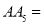 _____________ (用含
_____________ (用含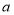 的最简代数式表示)
的最简代数式表示) (2)试写出线段
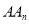 的长度(用含
的长度(用含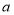 和
和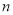 的代数式表示,无需说明理由)
的代数式表示,无需说明理由)
相关试题

