搜索
【题目】计算：
（1）
；
（2）
；
（3）
；
（4）
．
（5）
；
（6）
参考答案：
【答案】（1）15；（2）6；（3）3；（4）7；（5）2.32；（6）2．
【解析】
(1)先化简，再计算加减法即可求解；
(2)(5)(6)先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算；
(3)先算乘除，后算减法即可求解；
(4)根据乘法分配律简便计算．
(1)20+8(1)+(4)
=20+8+14
=24+9
=15；
(2)
×(
)2÷(0.5)3
=
=6；
(3)46÷(2)×()
=4+3×()
=41
=3；
(4)(36)×(
)
=36×
=1624+15
=7；
(5)(2)2×0.5(1.6)2÷(2)3
=4×0.52.56÷(8)
=2+0.32
=2.32；
(6)14÷(4)(
)2×(3)+|(1)22|
=1÷(4)
×(3)+|12|
=+
+1
=2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法中：①0是最小的整数；②有理数不是正数就是负数；③正整数、负整数、正分数、负分数统称为有理数；④非负数就是正数；④
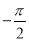不仅是有理数，而且是分数；⑤
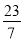是无限不循环小数，所以不是有理数；⑥无限小数不都是有理数；⑦正数中没有最小的数，负数中没有最大的数．其中错误的说法的个数为（ ）A. 7个B. 6个C. 5个D. 4个
-
科目： 来源： 题型：
查看答案和解析>>【题目】自主学习，请阅读下列解题过程．
解一元二次不等式：x2﹣5x＞0．
解：设x2﹣5x=0，解得：x1=0，x2=5，则抛物线y=x2﹣5x与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y=x2﹣5x的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即x2﹣5x＞0，所以，一元二次不等式x2﹣5x＞0的解集为：x＜0，或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
（1）上述解题过程中，渗透了下列数学思想中的 和 ．（只填序号）
①转化思想 ②分类讨论思想 ③数形结合思想
（2）一元二次不等式x2﹣5x＜0的解集为 ．
（3）用类似的方法解一元二次不等式：x2﹣2x﹣3＞0．
-
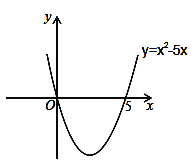
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线经过A（﹣1，0），B（5，0），C（0，
）三点．（1）求抛物线的解析式；
（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下面一列数，探究其中的规律：—1，
，
，
，
，
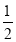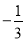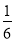
（1）填空：第11，12，13三个数分别是 ， ， ；
（2）第2020个数是什么？
（3）如果这列数无限排列下去，与哪个数越来越近？
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，数轴上三个点A、O、P，点O是原点，固定不动，点A和B可以移动，点A表示的数为
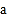，点B表示的数为
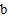.（1）若A、B移动到如图所示位置，计算
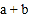的值.（2）在（1）的情况下，B点不动，点A向左移动3个单位长，写出A点对应的数
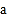，并计算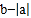
.（3）在（1）的情况下，点A不动，点B向右移动15.3个单位长，此时
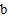比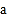大多少？请列式计算.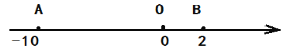
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个立方体的每个面上都标有数字1、2、3、4、5、6，根据图中该立方体A、B、C三种状态所显示的数字，可推出“？”处的数字是
相关试题
