【题目】观察下面一列数,探究其中的规律:—1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)填空:第11,12,13三个数分别是 , , ;
(2)第2020个数是什么?
(3)如果这列数无限排列下去,与哪个数越来越近?
参考答案:
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)0.
;(3)0.
【解析】
(1)把1等价于 ![]() ,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…,又知奇数项是负数,偶数项是正数,所以第11,12,13个数分别是-
,经观察发现每一项的分子分别是1,分母等于各自的序号,如分母分别是1,2,3,4,5,6…,又知奇数项是负数,偶数项是正数,所以第11,12,13个数分别是-![]() ,
,![]() ,-
,-![]() ;
;
(2)由(1)的分析可知第2020个数是 ![]() ;
;
(3)分子为1,分母越大,越接近0.
(1)将1等价于![]() ,即:
,即:![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
可以发现分子永远为1,分母等于序数,奇数项为负数,偶数项为正,由此可以推出第11,12,13个数分别是![]() ,
,![]() ,
,![]() ;
;
(2)第n个数是(1)n![]() ,
,
所以第2020个数为:(1)2020 ![]() ;
;
(3)如果这列数无限排列下去,与0越来越近。
故答案为:(1)![]() ,
,![]() ,
,![]() ;(2)
;(2)![]() ;(3)0.
;(3)0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】自主学习,请阅读下列解题过程.
解一元二次不等式:x2﹣5x>0.
解:设x2﹣5x=0,解得:x1=0,x2=5,则抛物线y=x2﹣5x与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=x2﹣5x的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集为:x<0,或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式x2﹣5x<0的解集为 .
(3)用类似的方法解一元二次不等式:x2﹣2x﹣3>0.
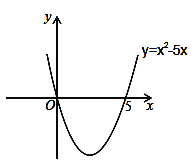
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,
 )三点.
)三点.(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)
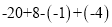 ;
;(2)
 ;
;(3)
 ;
;(4)
 .
.(5)
 ;
;(6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,数轴上三个点A、O、P,点O是原点,固定不动,点A和B可以移动,点A表示的数为
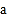 ,点B表示的数为
,点B表示的数为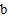 .
.(1)若A、B移动到如图所示位置,计算
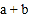 的值.
的值.(2)在(1)的情况下,B点不动,点A向左移动3个单位长,写出A点对应的数
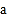 ,并计算
,并计算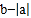 .
.(3)在(1)的情况下,点A不动,点B向右移动15.3个单位长,此时
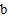 比
比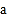 大多少?请列式计算.
大多少?请列式计算.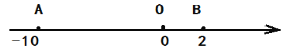
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个立方体的每个面上都标有数字1、2、3、4、5、6,根据图中该立方体A、B、C三种状态所显示的数字,可推出“?”处的数字是

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

相关试题

