【题目】在矩形ABCD中,AB=6cm,BC=8cm,若将矩形对角线BD对折,使B点与D点重合,四边形EBFD是菱形吗?请说明理由,并求这个菱形的边长. 
参考答案:
【答案】解:四边形EBFD是菱形, 理由:∵将矩形对角线BD对折,使B点与D点重合,
∴EF垂直平分BD,
∴BO=DO,
∵四边形ABCD是矩形,
∴AD=BC,
∴∠EDB=∠DBC,
∴∠DEF=∠EFB,
在△EOD和△FOB中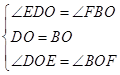 ,
,
∴△EOD≌△FOB(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形,
又∵BD⊥EF,
∴平行四边形BEDF是菱形;
设BE=x,
可得方程:62+(8﹣x)2=x2 ,
解得:x=6.25,
答:菱形的边长为6.25cm
【解析】首先利用翻折变换的性质得出BO=DO,进而得出∠DEF=∠EFB,求出△EOD≌△FOB,进而得出四边形BEDF是平行四边形,再利用BD⊥EF,得出平行四边形BEDF是菱形;利用菱形的性质以及勾股定理得出菱形的边长.
【考点精析】本题主要考查了菱形的判定方法和矩形的性质的相关知识点,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形;矩形的四个角都是直角,矩形的对角线相等才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
 (a>0,a为常数)和y=
(a>0,a为常数)和y=  在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=  的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=  的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=  的图象于点B,当点M在y=
的图象于点B,当点M在y=  的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 .
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是 . 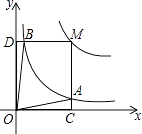
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA=
 ,cot∠ABC=
,cot∠ABC=  ,AD=8.
,AD=8.
(1)求⊙D的半径;
(2)求CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,拦水坝的横断面为梯形ABCD,AB∥CD,坝顶宽DC为6米,坝高DG为2米,迎水坡BC的坡角为30°,坝底宽AB为(8+2
 )米.
)米. 
(1)求背水坡AD的坡度;
(2)为了加固拦水坝,需将水坝加高2米,并且保持坝顶宽度不变,迎水坡和背水坡的坡度也不变,求加高后坝底HB的宽度. -
科目: 来源: 题型:
查看答案和解析>>【题目】应用探究题 在图①中,已知长方形的长和宽分别为a,b,将线段A1A2向右平移1个单位长度到B1B2的位置,得到封闭图形A1A2B2B1(即阴影部分).
在图②中,将折线A1A2A3向右平移1个单位长度到折线B1B2B3的位置,得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你画一条类似的有两个折点的折线,同样向右平移1个单位长度,从而得到一个封闭图形,并用阴影表示;
(2)请你分别写出前三个图形中除去阴影部分后剩余部分的面积:S1,S2,S3;
(3)联想与探索:
如图④,在一块长方形草地上,草地的长和宽仍分别为a,b,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位长度),请你猜想空白部分表示的草地面积是多少,并说明你的猜想是正确的.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD,点E在CB的延长线上,联结AE、DE,DE与边AB交于点F,FG∥BE且与AE交于点G.

(1)求证:GF=BF.
(2)在BC边上取点M,使得BM=BE,联结AM交DE于点O.求证:FOED=ODEF.
相关试题

