【题目】该怎样配杂拌糖

节日快到了,各家各户都在准备年货,糖果更是每家必备的年货.小丽的爸爸刚承包了一个副食店.他想:一定要抓住商机,薄利多销.为此他动了一番脑筋.如果把各种糖果混合起来配成杂拌糖,这样顾客就可以花较少的钱吃到各种口味的糖了.于是他把店里现有的6种售价为11元/千克的奶糖和6种售价为6元 /千克的水果糖混合在一起,配成100千克售价为8元/千克的杂拌糖,那么该取奶糖、水果糖各多少千克呢?小丽的爸爸想了半天,也没有解决这个问题.晚上回家后,只好请小丽帮忙.没想到女儿不到两分钟就找到了答案.
父亲按女儿的方法配好杂拌糖,开始卖了起来.顾客看到杂拌糖品种齐全,价格公道,都愿意来买.小店的生意还真红火.爸爸更是高兴得合不拢嘴,心里直夸聪明的女儿.你知道小丽告诉爸爸是怎样配杂拌糖的吗?
参考答案:
【答案】见解析
【解析】试题分析:设该取奶糖、水果糖各![]() 千克,
千克, ![]() 千克,根据千克数与钱数列出方程组,求出方程组的解即可得到结果.
千克,根据千克数与钱数列出方程组,求出方程组的解即可得到结果.
试题解析:设取![]() 千克奶糖,
千克奶糖, ![]() 千克水果糖.
千克水果糖.
根据题意有![]()
法一:由①得:y=100-x③.
将③代入②得:11x+6(100-x)=800.
∴x=40,∴y=100-x=60.
法二:①×6得:6x+6y=600④.
②-④得:5x=200,
∴x=40.
则y=100-40=60.
∴取6种奶糖共40千克,6种水果糖共60千克,混合制成杂拌糖.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某旅游景点三月份共接待游客25万人次,五月份共接待游客64万人次,设每月的平均增长率为x,则可列方程为( )
A.25(1+x)2=64
B.25+25(1+x)2=64
C.25(1+2x)=64
D.64(1﹣x2)=25 -
科目: 来源: 题型:
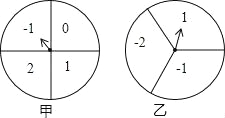
查看答案和解析>>【题目】如图,甲、乙分别是4等分、3等分的两个圆转盘,指针固定,转盘转动停止后,指针指向某一数字.
(1)直接写出转动甲盘停止后指针指向数字“1”的概率;
(2)小华和小明利用这两个转盘做游戏,两人分别同时转动甲、乙两个转盘,停止后,指针各指向一个数字,若两数字之积为非负数则小华胜;否则,小明胜.你认为这个游戏公平吗?请你利用列举法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】过多边形的一个顶点可以作7条对角线,则此多边形的内角和是外角和的( )
A. 4倍 B. 5倍 C. 6倍 D. 3倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了的三束气球(每束4个气球),每束价格如图所示.

(1)若笑脸气球的单价是x元,请用含x的代数式表示第②束、第③束气球的总价格;(要求化简后,填在图形中)
(2)若第②束气球的总价钱比第③束气球的总价钱少2元,求这两种类的气球的单价. -
科目: 来源: 题型:
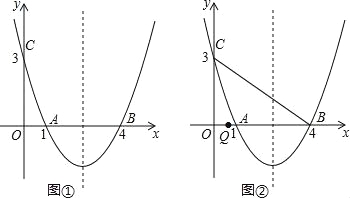
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
相关试题

