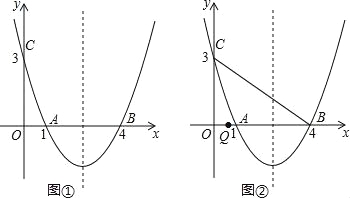
【题目】如图,抛物线y=ax2+bx+c经过A(1,0)、B(4,0)、C(0,3)三点.
(1)求抛物线的解析式;
(2)如图①,在抛物线的对称轴上是否存在点P,使得四边形PAOC的周长最小?若存在,求出四边形PAOC周长的最小值;若不存在,请说明理由.
(3)如图②,点Q是线段OB上一动点,连接BC,在线段BC上是否存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形?若存在,求点M的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x+3(2)9(3)(
x+3(2)9(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() )
)
【解析】
试题分析:(1)把点A(1,0)、B(4,0)、C(0,3)三点的坐标代入函数解析式,利用待定系数法求解;
(2)A、B关于对称轴对称,连接BC,则BC与对称轴的交点即为所求的点P,此时PA+PC=BC,四边形PAOC的周长最小值为:OC+OA+BC;根据勾股定理求得BC,即可求得;
(3)分两种情况分别讨论,即可求得.
试题解析:(1)根据题意设抛物线的解析式为y=a(x﹣1)(x﹣4),
代入C(0,3)得3=4a,
解得a=![]() ,
,
y=![]() (x﹣1)(x﹣4)=
(x﹣1)(x﹣4)=![]() x2﹣
x2﹣![]() x+3,
x+3,
所以,抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+3.
x+3.
(2)∵A、B关于对称轴对称,如图1,连接BC,
∴BC与对称轴的交点即为所求的点P,此时PA+PC=BC,
∴四边形PAOC的周长最小值为:OC+OA+BC,
∵A(1,0)、B(4,0)、C(0,3),
∴OA=1,OC=3,BC=![]() =5,
=5,
∴OC+OA+BC=1+3+5=9;
∴在抛物线的对称轴上存在点P,使得四边形PAOC的周长最小,四边形PAOC周长的最小值为9.
(3)∵B(4,0)、C(0,3),
∴直线BC的解析式为y=﹣![]() x+3,
x+3,
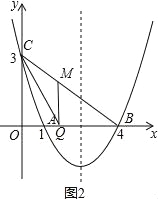
①当∠BQM=90°时,如图2,设M(a,b),
∵∠CMQ>90°,
∴只能CM=MQ=b,
∵MQ∥y轴,
∴△MQB∽△COB,
∴![]() ,
,
即![]() ,解得b=
,解得b=![]() ,代入y=﹣
,代入y=﹣![]() x+3得,
x+3得,![]() =﹣
=﹣![]() a+3,解得a=
a+3,解得a=![]() ,
,
∴M(![]() ,
,![]() );
);
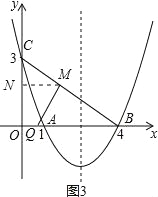
②当∠QMB=90°时,如图3,
∵∠CMQ=90°,
∴只能CM=MQ,
设CM=MQ=m,
∴BM=5﹣m,
∵∠BMQ=∠COB=90°,∠MBQ=∠OBC,
∴△BMQ∽△BOC,
∴![]() ,解得m=
,解得m=![]() ,
,
作MN∥OB,
∴![]() ,即
,即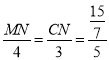
∴MN=![]() ,CN=
,CN=![]() ,
,
∴ON=OC﹣CN=3﹣![]() =
=![]() ,
,
∴M(![]() ,
,![]() ),
),
综上,在线段BC上存在这样的点M,使△CQM为等腰三角形且△BQM为直角三角形,点M的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】该怎样配杂拌糖

节日快到了,各家各户都在准备年货,糖果更是每家必备的年货.小丽的爸爸刚承包了一个副食店.他想:一定要抓住商机,薄利多销.为此他动了一番脑筋.如果把各种糖果混合起来配成杂拌糖,这样顾客就可以花较少的钱吃到各种口味的糖了.于是他把店里现有的6种售价为11元/千克的奶糖和6种售价为6元 /千克的水果糖混合在一起,配成100千克售价为8元/千克的杂拌糖,那么该取奶糖、水果糖各多少千克呢?小丽的爸爸想了半天,也没有解决这个问题.晚上回家后,只好请小丽帮忙.没想到女儿不到两分钟就找到了答案.
父亲按女儿的方法配好杂拌糖,开始卖了起来.顾客看到杂拌糖品种齐全,价格公道,都愿意来买.小店的生意还真红火.爸爸更是高兴得合不拢嘴,心里直夸聪明的女儿.你知道小丽告诉爸爸是怎样配杂拌糖的吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a、b、c是同一平面内三条不重合的直线,则它们的交点可以有( )
A.1个或2个或3个
B.0个或1个或2个或3个
C.1个或2个
D.以上都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】陈老师打算购买装扮学校“六一”儿童节活动会场,气球种类有笑脸和爱心两种.两种气球的价格不同,但同一种类的气球价格相同.由于会场布置需要,购买了的三束气球(每束4个气球),每束价格如图所示.

(1)若笑脸气球的单价是x元,请用含x的代数式表示第②束、第③束气球的总价格;(要求化简后,填在图形中)
(2)若第②束气球的总价钱比第③束气球的总价钱少2元,求这两种类的气球的单价. -
科目: 来源: 题型:
查看答案和解析>>【题目】周长相等的正三角形、正四边形、正六边形的面积S3、S4、S6间的大小关系是( )
A.S3>S4>S6 B.S6>S4>S3 C.S6>S3>S4 D.S4>S6>S3
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.两点之间的距离是两点间的线段
B.同一平面内,过一点有且只有一条直线与已知直线平行
C.与同一条直线垂直的两条直线也垂直
D.同一平面内,过一点有且只有一条直线与已知直线垂直 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球,在不允许将球倒出来数的前提下,小亮为了估计其中的红球数,采用如下方法:先将口袋中的球摇匀,再从口袋里随机摸出一球,记下颜色,然后把它放回口袋中,不断重复上述过程,小亮共摸了100次,其中有10次摸到白球.因此小亮估计口袋中的红球大约有( )个.
A.45
B.48
C.50
D.55
相关试题

