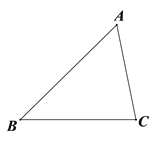
【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线![]() 和边BC的垂直平分线
和边BC的垂直平分线![]() (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);
(2)设(1)中的直线![]() 和直线
和直线![]() 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
参考答案:
【答案】(1)作图见解析;(2)证明见解析.
【解析】试题分析:
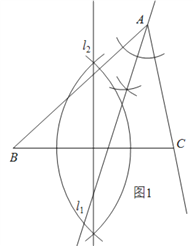
(1)如图1,用“尺规作图”作出∠ABC的角平分线,再反向延长即可得到![]() ;再用“尺规作图”作出BC的垂直平分线
;再用“尺规作图”作出BC的垂直平分线![]() 即可;
即可;
(2)如图2,连接PB、PC,由题意易证△PBE≌△PCF,从而可得BE=CF.
试题解析:
(1)如图1,图中直线![]() 和直线
和直线![]() 为题中所求直线;
为题中所求直线;
(2)如图2,连接PB、PC,
∵AP平分∠BAC,PE⊥AB于点E,PF⊥AC于点F,
∴PE=PF,∠PEB=∠PFC=90°,
∵![]() 垂直平分BC,点P在
垂直平分BC,点P在![]() 上,
上,
∴PB=PC,
∴△PBE≌△PCF,
∴BE=CF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是
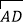 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,
b满足 |a+2|+
 =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).(1)求a,b的值及S三角形ABC;
(2)若点M在x轴上,且S三角形ACM=
 S三角形ABC,试求点M的坐标.
S三角形ABC,试求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.

(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )



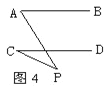
A. 、1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a1=0,an+1=﹣|an+n|(n≥1,且n为整数),则a2020的值为( )
A.2020B.﹣2020C.1010D.﹣1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.

相关试题

