【题目】如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.

参考答案:
【答案】(1)△DEF是等腰直角三角形. (2)仍然成立.
【解析】试题分析:
(1)连接CD,如图1,结合已知条件易证△AED≌△CFD,由此即可证得DE=DF,∠EDF=90°,从而可得△DEF是等腰直角三角形;
(2)先根据题意画出符合要求的图形,如图2,连接CD,结合已知条件易证△AED≌△CFD,由此即可证得;DE=DF,∠EDF=90°,从而可得此时△DEF仍然是等腰直角三角形.
试题解析:
(1)△DEF是等腰直角三角形,理由如下:
如图1,连接CD,
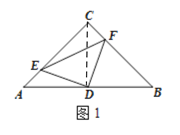
∵AC=BC,∠ACB=90°,点D是BC边的中点,
∴CD⊥BC,∠A=∠DCF=45°,CD=![]() BC=AD,
BC=AD,
又∵AE=CF,
∴△AED≌△CFD,
∴DE=DF,∠ADE=∠CDF,
又∵CD⊥BC,
∴∠CFD+∠CDE=∠ADE+∠CDE=∠CDA=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
(2)如图2,(1)中结论仍然成立,理由如下:
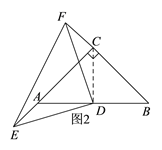
连接CD,∵AC=BC,∠ACB=90°,点D是BC边的中点,
∴CD⊥BC,∠A=∠DCB=45°,CD=![]() BC=AD,
BC=AD,
∴∠EAD=180°+45°=135°,∠ACD=180°-45°=135°,
又∵AE=CF,
∴△AED≌△CFD,
∴DE=DF,∠ADE=∠CDF,
又∵CD⊥BC,
∴∠ADE+∠ADF=∠CDF+∠ADF=∠CDA=90°,即∠EDF=90°,
∴△DEF是等腰直角三角形;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC.
(1)用直尺和圆规作∠A的平分线所在的直线
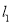 和边BC的垂直平分线
和边BC的垂直平分线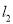 (要求:不写作法,保留画图痕迹);
(要求:不写作法,保留画图痕迹);(2)设(1)中的直线
 和直线
和直线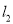 交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.
交于点P,过点P作PE⊥AB,垂足为点E,过点P作PF⊥AC交AC的延长线于点F.请探究BE和CF的数量关系,并说明理由.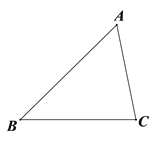
-
科目: 来源: 题型:
查看答案和解析>>【题目】①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )



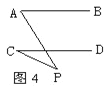
A. 、1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a1=0,an+1=﹣|an+n|(n≥1,且n为整数),则a2020的值为( )
A.2020B.﹣2020C.1010D.﹣1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】单项式﹣3πx6y的系数是_____.
-
科目: 来源: 题型:
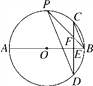
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边△ABC和⊙M.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证: AM∥BC;
(2)如图2,若⊙M与BA的延长线AK、BC的延长线CF及边AC均相切,求证:四边形ABCM是平行四边形.

相关试题

