【题目】已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。
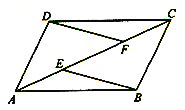
求证:(1)△ADF≌△CBE
(2)EB∥DF.
参考答案:
【答案】∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC. ………………(1分)
∴∠DAC=∠BCE.
又∵AE=CF,∴AF=CE
∴△ADF≌△CBE.……………………(4分)
∴∠AFD=∠CEB.
∴BE∥DF. ……………………………(6分
【解析】试题分析:要证△ADF≌△CBE,因为AE=CF,则两边同时加上EF,得到AF=CE,又因为ABCD是平行四边形,得出AD=CB,∠DAF=∠BCE,从而根据SAS推出两三角形全等,由全等可得到∠DFA=∠BEC,所以得到DF∥EB.
证明:(1)∵AE=CF,
∴AE+EF=CF+FE,即AF=CE.
又ABCD是平行四边形,
∴AD=CB,AD∥BC.
∴∠DAF=∠BCE.
在△ADF与△CBE中![]() ,
,
∴△ADF≌△CBE(SAS).
(2)∵△ADF≌△CBE,
∴∠DFA=∠BEC.
∴DF∥EB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知3n-2m-1=3m-2n,运用等式的性质,试比较m与n的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三人中有两人性别相同的概率是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段话,并解决后面的问题.
观察下面一列数:1,2,4,8,……我们发现,这列数从第二项起,每一项与它前一项的比值都是2.我们把这样的一列数叫做等比数列,这个共同的比值叫做等比数列的公比.
(1)等比数列5,-10,20,……的第4项是_____________;
(2)如果一列数
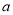 1,
1, 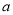 2,
2, 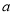 3,……是等比数列,且公比是q,那么根据上述规定有
3,……是等比数列,且公比是q,那么根据上述规定有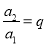 ,
, 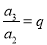 ,
, 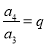 ,……因此,可以得到
,……因此,可以得到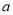 2=
2= 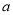 1q,
1q,  3=
3= 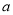 2q=
2q= 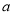 1q·q=
1q·q= 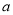 1q2,
1q2, 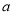 4=
4= 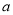 3q=
3q=  1q2·q=
1q2·q= 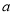 1q3,……则
1q3,……则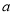 n=____________;(用含
n=____________;(用含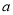 1与q的代数式表示)
1与q的代数式表示)(3)一个等比数列的第2项是6,第3项是-18,求它的第1项和第4项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图方式放置,点A1、A2、A3…和点C1、C2、C3…分别在直线
 和x轴上。已知点B1(1,1)、B2(3,2),请写出点B3的坐标是___________,点Bn的坐标是_______________。
和x轴上。已知点B1(1,1)、B2(3,2),请写出点B3的坐标是___________,点Bn的坐标是_______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的个数是( )
①过两点有且只有一条直线; ②两直线相交只有一个交点;
③0的绝对值是它本身 ④射线AB和射线BA是同一条射线.
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )
A. y=(x﹣1)2+2 B. y=(x﹣1)2+3
C. y=(x﹣2)2+2 D. y=(x﹣2)2+4
相关试题

