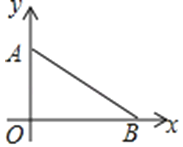
【题目】如图,在平面直角坐标系中,点A在x轴上,坐标为(0,3),点B在x轴上.
(1)在坐标系中求作一点M,使得点M到点A,点B和原点O这三点的距离相等,在图中保留作图痕迹,不写作法;
(2)若sin∠OAB=![]() ,求点M的坐标.
,求点M的坐标.
参考答案:
【答案】(1)作图见解析;(2)(2,![]() ).
).
【解析】整体
(1)直角三角形斜边上的中点到三个顶点的距离相等;(2)根据OA=3,sin∠OAB=![]() 求出B的坐标,再由M是AB的中点,求点M的坐标.
求出B的坐标,再由M是AB的中点,求点M的坐标.
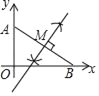
解:(1)如图所示:点M,即为所求;
(2)∵sin∠OAB=![]() ,
,
∴设OB=4x,AB=5x,
由勾股定理可得:32+(4x)2=(5x)2,
解得:x=1,
∴OB=4,由B(4,0),
由作图可得:M为AB的中点,则M的坐标为:(2,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
-
科目: 来源: 题型:
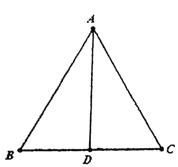
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC的中点,则下列结论正确的是( )
①△ABD≌△ACD;②∠B=∠C;③∠BAD=∠CAD;④AD⊥BC
A. ①②③B. ②③④C. ①②④D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现有一个均匀的转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
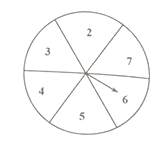
求:(1)转动转盘,转出的数字大于3的概率是多少?
(2)现有两张分别写有3和4的卡片,随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
①这三条线段能构成三角形的概率是 .
②这三条线段能构成等腰三角形的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某生在旗杆EF与实验楼CD之间的A处,测得∠EAF=60°,然后向左移动12米到B处,测得∠EBF=30°,∠CBD=45°,sin∠CAD=
 .
.(1)求旗杆EF的高;
(2)求旗杆EF与实验楼CD之间的水平距离DF的长.

-
科目: 来源: 题型:
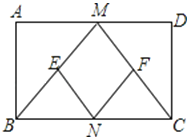
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
相关试题

