【题目】孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.
参考答案:
【答案】
(1)
解:设A种树每棵x元,B种树每棵y元,
依题意得: ![]() ,
,
解得 ![]() .
.
答:A种树每棵100元,B种树每棵80元;
(2)
解:设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,
则a≥3(100﹣a),
解得a≥75.
设实际付款总金额是y元,则
y=0.9[100a+80(100﹣a)],即y=18a+7200.
∵18>0,y随a的增大而增大,
∴当a=75时,y最小.
即当a=75时,y最小值=18×75+7200=8550(元).
答:当购买A种树木75棵,B种树木25棵时,所需费用最少,最少为8550元.
【解析】(1)设A种树每棵x元,B种树每棵y元,根据“购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元”列出方程组并解答;(2)设购买A种树木为a棵,则购买B种树木为(100﹣a)棵,根据“购买A种树木的数量不少于B种树木数量的3倍”列出不等式并求得a的取值范围,结合实际付款总金额=0.9(A种树的金额+B种树的金额)进行解答.本题考查了一次函数的应用和二元一次方程组的应用.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第( )秒
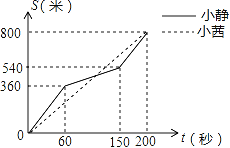
A. 80 B. 105 C. 120 D. 150
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的数阵是由50个偶数排成的.
(1)图中框内的4个数有什么关系?
(2)在数阵图中任意作一类似于(1)中的框,设其中的一个数为
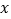 ,那么其他三个数怎样表示?
,那么其他三个数怎样表示?(3)如果四个数的和是172,能否求出这4个数?
(4)如果四个数的和是322,能否求出这4个数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象经过点A(6,﹣3)和点B(﹣2,5).
(1)求这个一次函数的表达式.
(2)求该函数图象与坐标轴围成的三角形的面积.
(3)判断点C(2,2)是在直线AB的上方(右边)还是下方(左边).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
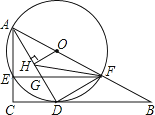
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径. -
科目: 来源: 题型:
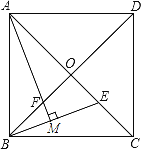
查看答案和解析>>【题目】如图,正方形ABCD的边长为2
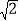 ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.
,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作AM⊥BE于点M,交BD于点F.(1)求证:AF=BE;
(2)求点E到BC边的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(﹣1,﹣4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
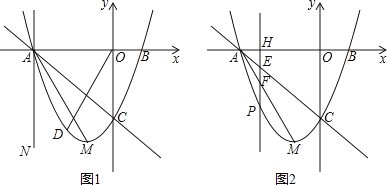
(1)填空:b= , c= , 直线AC的解析式为
(2)直线x=t与x轴相交于点H.
①当t=﹣3时得到直线AN(如图1),点D为直线AC下方抛物线上一点,若∠COD=∠MAN,求出此时点D的坐标;
②当﹣3<t<﹣1时(如图2),直线x=t与线段AC,AM和抛物线分别相交于点E,F,P.试证明线段HE,EF,FP总能组成等腰三角形;如果此等腰三角形底角的余弦值为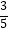 ,求此时t的值.
,求此时t的值.
相关试题

