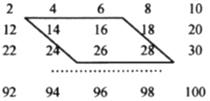
【题目】如图所示的数阵是由50个偶数排成的.
(1)图中框内的4个数有什么关系?
(2)在数阵图中任意作一类似于(1)中的框,设其中的一个数为![]() ,那么其他三个数怎样表示?
,那么其他三个数怎样表示?
(3)如果四个数的和是172,能否求出这4个数?
(4)如果四个数的和是322,能否求出这4个数?
参考答案:
【答案】(1)框中同行中的两个数都相差2,第二行的两个数与第一行相应的两个数都相差12;(2)其他三个数可表示为![]() ;(3)这四个数分别是36,38,48,50;(4)不存在这样的4个数.理由见解析.
;(3)这四个数分别是36,38,48,50;(4)不存在这样的4个数.理由见解析.
【解析】
(1)可利用图例,看出框内四个数字之间的关系,框中同行中的两个数都相差2,第二行的两个数与第一行相应的两个数都相差12;
(3)利用和为172作为相等关系可求出四个数的具体值;
(4)利用上述规律可知四个数的和不可以是322.
(1)观察数阵图中数的规律发现,框中同行中的两个数都相差2,第二行的两个数与第一行相应的两个数都相差12;
(2)不妨设左上角的数为![]() ,则其他三个数可表示为
,则其他三个数可表示为![]() ;
;
(3)设左上角的数为![]() ,
,
由题意,得![]() ,
,
解得![]() .
.
所以这四个数分别是36,38,48,50;
(4)不存在这样的4个数.理由如下:
设左上角的数为![]() ,则其他三个数可表示为
,则其他三个数可表示为![]() ,
,
由题意,得![]() ,
,
解得![]() ,
,
不合题意.
故不存在这样的4个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10.动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数 ;当t=3时,OP=
(2)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时追上点P?
(3)动点R从点B出发,以每秒8个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多少秒时PR相距2个单位长度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1 , x2 .
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为增强学生体质,某中学在体育课中加强了学生的长跑训练.在一次女子800米耐力测试中,小静和小茜在校园内200米的环形跑道上同时起跑,同时到达终点;所跑的路程S(米)与所用的时间t(秒)之间的函数图象如图所示,则她们第一次相遇的时间是起跑后的第( )秒
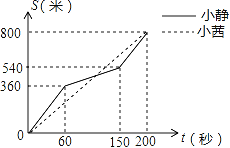
A. 80 B. 105 C. 120 D. 150
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象经过点A(6,﹣3)和点B(﹣2,5).
(1)求这个一次函数的表达式.
(2)求该函数图象与坐标轴围成的三角形的面积.
(3)判断点C(2,2)是在直线AB的上方(右边)还是下方(左边).

-
科目: 来源: 题型:
查看答案和解析>>【题目】孝感市在创建国家级园林城市中,绿化档次不断提升.某校计划购进A,B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元.
(1)求A种,B种树木每棵各多少元?
(2)因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价九折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
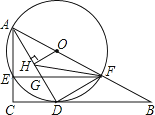
(1)求证:AD平分∠CAB;
(2)若OH⊥AD于点H,FH平分∠AFE,DG=1.
①试判断DF与DH的数量关系,并说明理由;
②求⊙O的半径.
相关试题

