【题目】某中学组织全体学生参加了“走出校门,服务社会”的活动,活动分为打扫街道,去敬老院服务和到社区文艺演出三项.从七年级参加活动的同学中抽取了部分同学,对打扫街道,去敬老院服务和到社区文艺演出的人数进行了统计,并绘制了直方图和扇形统计图.请解决以下问题:
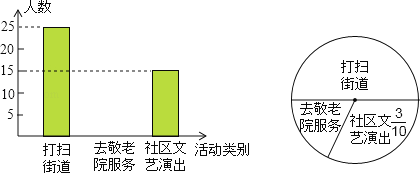
(1)求抽取的部分同学的人数;
(2)补全直方图的空缺部分;
(3)若七年级有200名学生,估计该年级去敬老院的人数.
参考答案:
【答案】(1)50人,(2)见解析;(3)40人
【解析】
试题分析:(1)依据总数=频数÷百分比求解即可;
(2)先求得去敬老院的人数,然后补全统计图即可;
(3)先求得去敬老院的人数所占的比例,然后再乘以200即可.
解:(1)15÷![]() =50人;
=50人;
共抽取了50人.
(2)50﹣25﹣15=10.
补全条形统计图如图所示:
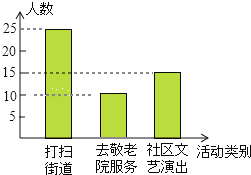
(3)10÷50×200=40人
该年级去敬老院的人数约为40人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=1是方程ax2+x﹣6=0的一个根,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若3xm+5y2与x3yn的和是单项式,则mn= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】课本拓展
旧知新意:
我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
1.尝试探究:
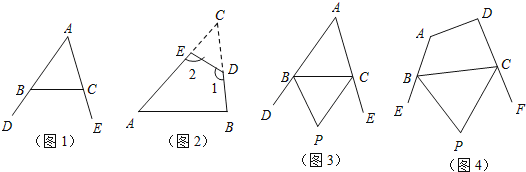
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
2.初步应用:
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2-∠C= ;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
3拓展提升:
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.

(1)求证:OE=OF.
(2)当∠DOE等于 度时,四边形BFDE为菱形。(直接填写答案即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)|-1|+(-2)3+(7-π)0-(-
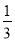 )-2
)-2(2)(-2x2)3+x2x4-(-3x3)2
(3)(p-q)4·(q-p)3·(p-q)2
(4)已知am=2,an=4,求a3m+2n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)

相关试题

