【题目】某体育用品商店老板到体育商场批发篮球、足球、排球共![]() 个,得知该体育商场篮球、足球、排球平均每个
个,得知该体育商场篮球、足球、排球平均每个![]() 元,篮球比排球每个多
元,篮球比排球每个多![]() 元,排球比足球每个少
元,排球比足球每个少![]() 元.
元.
(1) 求出这三种球每个各多少元;
(2) 经决定,该老板批发了这三种球的任意两种共![]() 个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
个,共花费了1060元,问该老板可能买了哪两种球?各买了几个;
(3) 该老板打算将每一种球各提价![]() 元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
元后,再进行打折销售,若排球、足球打八折,篮球打八五折,在(2)的情况下,为获得最大利润,他批发的一定是哪两种球?各买了几个?计算并说明理由.
参考答案:
【答案】(1)篮球每只40元,足球38元,排球30元;(2)若买的是足球和排球则求得可以是买足球20,排球10只;若买的是篮球和排球则是篮球16只,排球14只;(3)买篮球16只,排球14只利润最大.
【解析】
(1)分别设篮球每只x元,足球y,排球z,根据题意可得出三个二元一次不定方程,联立求解即可得出答案.
(2)假设:①买的是篮球和足球,分别为a只和b只,根据题意可得出两个方程,求出解后可判断出是否符合题意,进而再用同样的方法判断其他的符合题意的情况;
(3)分别对两种情况下的利润进行计算,然后比较利润的大小即可得出答案.
(1)设篮球每只x元,足球y,排球z,得
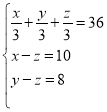 ;
;
解得x=40;y=38;z=30;
故篮球每只40元,足球38元,排球30元;
(2)假设:①买的是篮球和足球,分别为a只和b只,则
![]() ;
;
解得![]() ,则不可能是这种情况;
,则不可能是这种情况;
同理若买的是足球和排球则求得可以是买足球20,排球10只;
若买的是篮球和排球则是篮球16只,排球14只;
(3)对两种情况分别计算,若为足球和排球,即(38+20)×0.8×20+(30+20)0.8×10=1328(元);
若为篮球和排球,即(40+20)×0.85×16+(30+20)×0.8×14=1376(元),
∴买篮球16只,排球14只利润最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依次类推,图10中有10个直角三角形的内切圆,它们的面积分别记为
 ,
, ,
, ,…,
,…,  ,则
,则 = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在八年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调查.
问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.
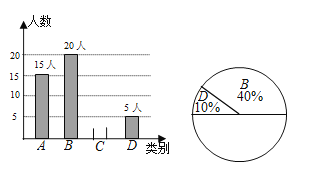
请根据上述信息解答下列问题:
(1)该班参与问卷调查的人数有 人;补全条形统计图;
(2)求出C类人数占总调查人数的百分比及扇形统计图中
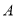 类所对应扇形圆心角的度数.
类所对应扇形圆心角的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)如图,已知直线
 和双曲线
和双曲线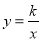 (k>0),点A(m,n)在双曲线
(k>0),点A(m,n)在双曲线  上.当m=n=2时.
上.当m=n=2时.(1)直接写出k的值;
(2)将直线
 作怎样的平移能使平移后的直线与双曲线
作怎样的平移能使平移后的直线与双曲线  只有一个交点.
只有一个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠A=∠C=45°,∠ADB=∠ABC=105°.
(1)若AD=2,求AB;
(2)若AB+CD=2
 +2,求AB.
+2,求AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在长方体
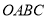 中,
中,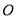 为平面直角坐标系的原点,
为平面直角坐标系的原点,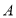 ,
,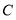 两点的坐标分别为
两点的坐标分别为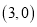 ,
,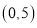 ,点
,点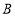 在第一象限.
在第一象限.(1) 写出
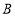 点坐标;
点坐标;(2) 若过点
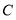 的直线
的直线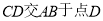 ,且把
,且把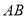 分为
分为 :
: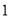 两部分,求出点
两部分,求出点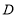 的坐标;
的坐标;(3) 在(2)的条件下,求出四边形
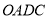 的面积;
的面积;(4) 若点
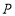 是射线
是射线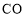 上的点,请直接写出
上的点,请直接写出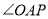 ,
,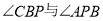 之间的数量关系.
之间的数量关系.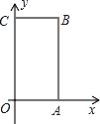
相关试题

