【题目】如图,在平面直角坐标系中,二次函数y=ax2+bx﹣4(a≠0)的图象与x轴交于A(﹣2,0)、C(8,0)两点,与y轴交于点B,其对称轴与x轴交于点D.
(1)求该二次函数的解析式;
(2)如图1,连结BC,在线段BC上是否存在点E,使得△CDE为等腰三角形?若存在,求出所有符合条件的点E的坐标;若不存在,请说明理由;
(3)如图2,若点P(m,n)是该二次函数图象上的一个动点(其中m>0,n<0),连结PB,PD,BD,求△BDP面积的最大值及此时点P的坐标.

参考答案:
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣4;(2)(8﹣2
x﹣4;(2)(8﹣2![]() ,﹣
,﹣![]() )、(0,﹣4)、(
)、(0,﹣4)、(![]() ,﹣
,﹣![]() );(3)(
);(3)(![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)根据待定系数法,可得函数解析式;
(2)分类讨论:当CD=DE时,当EC=DE时,当CD=CE时,根据等腰三角形的定义,可得关于m的方程,根据解方程,可得答案.
(3)根据题意得,点P的坐标为(m, ![]() m2-
m2-![]() m-4),根据梯形的面积公式和三角形的面积公式计算求出△BDP面积,根据二次函数的性质解答.
m-4),根据梯形的面积公式和三角形的面积公式计算求出△BDP面积,根据二次函数的性质解答.
试题解析:(1)∵二次函数y=ax2+bx-4(a≠0)的图象与x轴交于A(-2,0)、C(8,0)两点,
∴![]() ,
,
解得![]() ,
,
∴该二次函数的解析式为y=![]() x2-
x2-![]() x-4;
x-4;
(2)在线段BC上是存在点E,使得△CDE为等腰三角形,
由二次函数y=![]() x2-
x2-![]() x-4可知对称轴x=3,
x-4可知对称轴x=3,
∴D(3,0).
∵C(8,0),
∴CD=5.
由二次函数y=![]() x2-
x2-![]() x-4可知B(0,-4).
x-4可知B(0,-4).
设BC的解析式为y=kx+b,
将B、C点坐标代入,得
![]() ,
,
解得![]() ,
,
BC的解析式为y=![]() x-4.
x-4.
E在线段BC上,设E点坐标为(m, ![]() m-4).
m-4).
①当CD=DE时,即(m-3)2+(![]() m-4)2=25,解得m1=0,m2=8(不符合题意舍去),
m-4)2=25,解得m1=0,m2=8(不符合题意舍去),
当m=0时, ![]() m-4=-4,
m-4=-4,
∴E1(0,-4);
②当EC=DE时,(m-8)2+(![]() m-4)2=(m-3)2+(
m-4)2=(m-3)2+(![]() m-4)2,解得m3=
m-4)2,解得m3=![]() ,
,
当m=![]() 时,
时, ![]() m-4=
m-4=![]() ×
×![]() -4=-
-4=-![]() ,
,
∴E2(![]() ,-
,-![]() );
);
③当CD=CE时,(m-8)2+(![]() m-4)2=25,解得m4=8+2
m-4)2=25,解得m4=8+2![]() ,m5=8-2
,m5=8-2![]() (不符合题意舍),
(不符合题意舍),
当m=8+2![]() 时,
时, ![]() m-4=
m-4=![]() ,即E3(8+2
,即E3(8+2![]() ,
, ![]() );
);
综上所述:所有符合条件的点E的坐标为E1(0,-4); E2(![]() ,-
,-![]() );E3(8+2
);E3(8+2![]() ,
, ![]() ).
).
(3)点P的坐标为(m, ![]() m2-
m2-![]() m-4),
m-4),
y=![]() m2-
m2-![]() m-4=
m-4=![]() (m-3)2-
(m-3)2-![]() ,
,
△BDP面积=![]() ×(4-
×(4-![]() m 2+
m 2+![]() m-4)×m-
m-4)×m-![]() ×3×4-
×3×4-![]() ×(m-3)×(-
×(m-3)×(-![]() m2+
m2+![]() m+4)
m+4)
=-![]() m2+
m2+![]() m=-
m=-![]() (m-
(m-![]() )2+
)2+![]() ,
,
∴当m=![]() 时,△BDP面积的最大,此时点P的坐标为(
时,△BDP面积的最大,此时点P的坐标为(![]() ,
, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】以3和-2为根的一元二次方程是______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b,c是三角形ABC的三边的长,且满足a2+2b2+c2-2b(a+c)=0,试判断此三角形三边的大小关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A.两名同学5次成绩的平均分相同,则方差较大的同学成绩更稳定
B.某班选出两名同学参加校演讲比赛,结果一定是一名男生和一名女生
C.学校气象小组预报明天下雨的概率为0.8,则明天下雨的可能性较大
D.为了解我是学校“阳光体育”活动开展情况,必须采用普查的方式 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,必然事件是( )
A.打开电视,正在播放新闻
B.抛一枚硬币,正面朝上
C.明天会下雨
D.地球绕着太阳转 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )
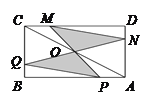
A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读新知:移项且合并同类项之后,只含有偶次项的四次方程称作双二次方程.其一般形式为ax4+bx2+c=0(a≠0),一般通过换元法解之,具体解法是设 x2=y,则原四次方程化为一元二次方程:ay2+by+c=0,解出y之后代入x2=y,从而求出x的值.例如解:4x4﹣8y2+3=0
解:设x2=y,则原方程可化为:4y2﹣8y+3=0
∵a=4,b=﹣8,c=3
∴b2﹣4ac=﹣(﹣8)2﹣4×4×3=16>0
∴y=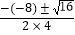 =
= 
∴y1= ,
,
∴y2=
∴当y1= 时,x2=
时,x2= 
∴x1= ,x2=﹣
,x2=﹣  ;当y1=
;当y1=  时,x2=
时,x2= 
∴x3=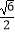 ,x4=﹣
,x4=﹣ 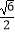
小试牛刀:请你解双二次方程:x4﹣2x2﹣8=0
归纳提高:思考以上解题方法,试判断双二次方程的根的情况,下列说法正确的是(选出所有的正确答案)
①当b2﹣4ac≥0时,原方程一定有实数根;②当b2﹣4ac<0时,原方程一定没有实数根;③当b2﹣4ac≥0,并且换元之后的一元二次方程有两个正实数根时,原方程有4个实数根,换元之后的一元二次方程有一个正实数根一个负实数根时,原方程有2个实数根;④原方程无实数根时,一定有b2﹣4ac<0.
相关试题

