Question

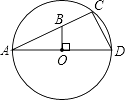
【题目】如图，AB是⊙O的直径，点D在AB的延长线上，BD=OB，点C在圆上，∠CAB=30°．

（1）求证：DC是⊙O的切线．
（2）若BD=1cm，求AC的长．

Answer 1

【答案】
（1）证明：连接OC、BC，如图，

∵AB是⊙O的直径，

∴∠ACB=90°，

∵OA=OC，

∴∠OCA=∠A=30°，

∴∠COB=∠A+∠OCA=60°，

∵OC=OB，

∴△OBC 是等边三角形，

∴∠OCB=∠OBC=60°，

又∵BD=OB，

∴∠BDC=∠BCD，

而∠OBC=∠BDC+∠BCD，

∴∠BCD=30°，

∴∠OCD=∠OCB+∠BCD=90°，

∴OC⊥CD，

∴DC是⊙O的切线

（2）解：OB=BD=BC=1，

在Rt△ABC中，∴∠A=30°，

∴AC= BC= cm

【解析】（1）连接OC、BC，如图，利用圆周角定理得到∠ACB=90°，则可计算出∠COB=60°，于是可判断△OBC 是等边三角形，则∠OCB=∠OBC=60°，再利用等腰三角形的性质和三角形外角性质计算出∠BCD=30°，从而得到∠OCD=90°，然后根据切线的判定定理可得到结论；（2）利用等边三角形的性质得OB=BD=BC=1，然后在Rt△ABC中利用含30度的直角三角形三边的关系可计算出AC．
【考点精析】根据题目的已知条件，利用圆周角定理和切线的判定定理的相关知识可以得到问题的答案，需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半；切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线．